前言
开源世界本身就是一个开放的生态,新的思想和工具不断被引入,同时老的技术及工具也在不断被淘汰,正是这种新旧更替促成了当前Linux的缤纷世界。整个开源运动及Linux内核的发展史,就是一部引人入胜且让人心怀澎湃的励志故事。
本文将聚焦Linux系统动态追踪技术框架的演化及各种框架的更替,重点介绍众多追踪术框架底层所依赖的内核层上的探测技术及手段,并结合Elkeid HIDS项目,展示系统安全产品如何利用这些手段达成针对攻击行为的检测以及攻击路径的可视化。Elkeid 是火山引擎面向客户输出的终端安全能力模型和应对主机、容器与容器集群、Serverless 等多种工作负载安全需求的开源解决方案。Elkeid源于字节跳动内部最佳实践,其出发点就是字节自身随着业务快速发展所面临的多云、云原生、多种工作负载共存情况下的安全需求。
1 Linux追踪技术演化
Linux系统提供了多种动态追踪技术框架,如最常用的有perf、SystemTap,以及由大神Brendan Gregg主导开发的BCC(BPF Compiler Collection)工具集等。不仅仅是技术框架种类上的繁杂,框架名称就可能是有着多重意义的复合概念,如果再考虑到不同的发行版上的支持及预装,更让人无所适从,即使是运维人员、靠性工程师、或者开发者中的老手在面对实际问题时也要思虑一番才能决定到底用哪个工具链方能最高效地定位并解决问题。
1.1 Linux追踪技术时间线
我们先从时间线上来理解Linux追踪技术的演化:
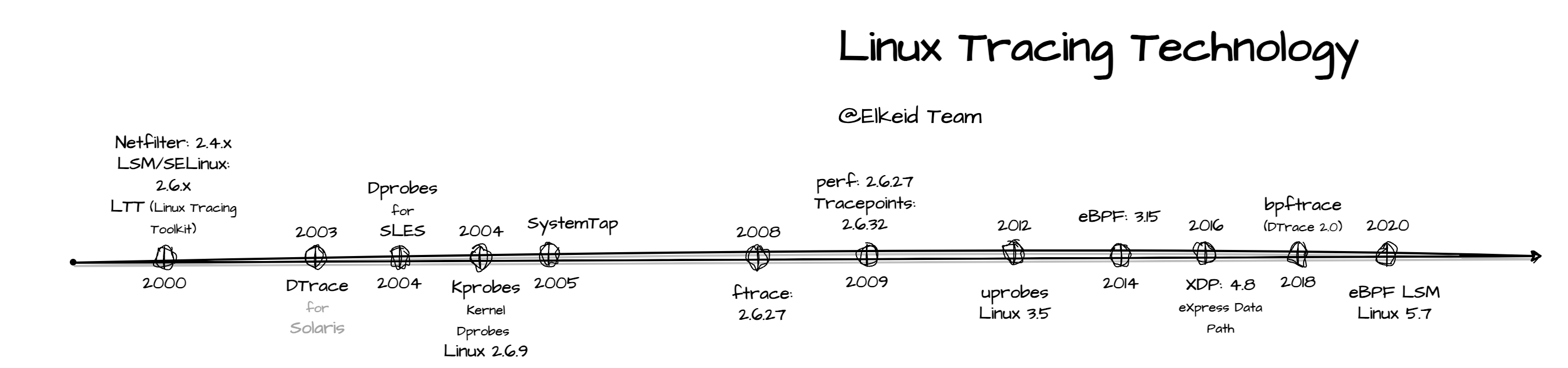
这个时间线是自2000年以来Linux内核追踪技术的演化过程,正是Linux开放的生态才促成了多种追踪框架不断涌现和更迭的局面,完美诠释了百花齐放、优胜劣汰的开源法则。
- 2000年初:在这个时期Linux内核还没有完整的追踪框架,但网络及安全上的需求一直在推动着Linux内核的追踪及探测能力的发展,如NSA SELinux安全模块引入了LSM Hooks回调机制并成为后续的安全模块如AppArmor所依赖的基础,网络层则是netfilter框架的引入以替代旧有的ipchains框架。
- Linux Trace Toolkit(LTT):LTT是最早的系统追踪和事件分析的框架之一,提供了Linux内核追踪的初始基础设施。LTT的开发早在1998年就已启动,但最终没能并入内核。之后又迎来了LTTng,即Linux Trace Toolkit Next Generation,LTTng提供了更好的扩展性、易用性以及更好的性能。LTTng其实并不是LTT的延续,而是对LTT整个框架的重写并一直维护至今。
- DTrace for Sun Solaris: 于2003年正式发布,其强大的功能及可定制性触动了整个Linux开发者圈子,此时Linux的内核跟踪框架缺失的问题开始引起更广泛的关注。
- IBM等公司开发了Dprobes for Linux,Linux发行版SLES最早引入此框架,直到2006年由SystemTap替代。Dprobes最终没能整合至Linux内核主线,但还是给Linux内核带来了Kprobes技术框架。
- Redhat公司于2005年引入了SystemTap框架,SystemTap是Redhat的Dtrace for Linux解决方案,SystemTap提供给开发者更强大且灵活的接口,允许开发者编写自定义脚本来追踪特定事件和分析系统执行。
- Ftrace:2008年左右Ftrace作为一个函数追踪器开始崭露头角,并最终成为Linux内核事实上的基准追踪框架。Ftrace允许记录函数调用及返回时的堆栈和时间戳等信息,为开发者提供了内核执行流的洞察能力。
- Perf:全称为Performance Counters for Linux,又被称作是Perf events 或 Perf tools,2009年作为性能分析工具被引入,Perf使用了硬件性能计数器,可提供性能分析、指令级追踪和统计抽样等功能,最终成为Linux系统事实上的性能分析基准工具。
- eBPF和BCC:近年来eBPF(扩展Berkeley包过滤器)的引入以及BPF编译器集合(BCC)的出现彻底改变了Linux内核追踪。eBPF允许在内核中进行动态追踪和执行自定义程序,而BCC提供了一系列用于编写和运行eBPF程序的工具和库。
Linux内核追踪从有限且分散的工具及方法最终发展出了全面且多功能的追踪基础设施,如Ftrace、Perf、SystemTap、LTTng、eBPF和BCC等,正是这些框架的引入为开发者带来追踪和分析Linux内核行为和性能的便利。
开源世界本身就是一个开放的生态,不断有新的思想和工具被引入,同时也不断有老的技术及老的工具被淘汰,正是这种更替促成了当前Linux的缤纷世界。整个开源运动及Linux内核的发展史就是一部引人入胜且让人心怀澎湃的故事,有兴趣的读者可延伸阅读参考资料[OS01: Rebel Code: Linux And The Open Source Revolution]。
1.2 追踪技术基础概念
在开始之前我们先澄清几个常用概念,这个概念很容易被混淆在一起:
Probing (探测):
可以将探测理解为在指定点的进行监控或测量,其核心在于插桩机制(instrumentation),可以提供在指令流特定位置添加和执行附加逻辑以采集相关数据的能力。Kprobes及uprobes,以及ftrace (Function hooks) 都有着各自的探测机制。
Tracing (跟踪):
跟踪所强调的事件捕获及数据收集能力,其目的是为了更好地理解软件系统的内部动作。如果将探测假设成为各个分支路径上的路标的话,跟踪就是通过这些路标所串起来的运行轨迹。
Profiling (性能分析):
性能分析也是基于数据采样的,但其的是为了评估和测量应用程序或系统性能指标,如执行时间、CPU/内存等相关资源的占用等。如通过分析性能分析器所输出的观测事件的统计图表,我们可以更方便地发现执行时间最长的函数等等。
Linux系统动态追踪框架其实都包含了以上三各能力,只不过倾向性有所不同,如perf强于性能分析及热点定位,而trace-cmd/ftrace则更多被用于事件跟踪及执行探查。
2 分层架构
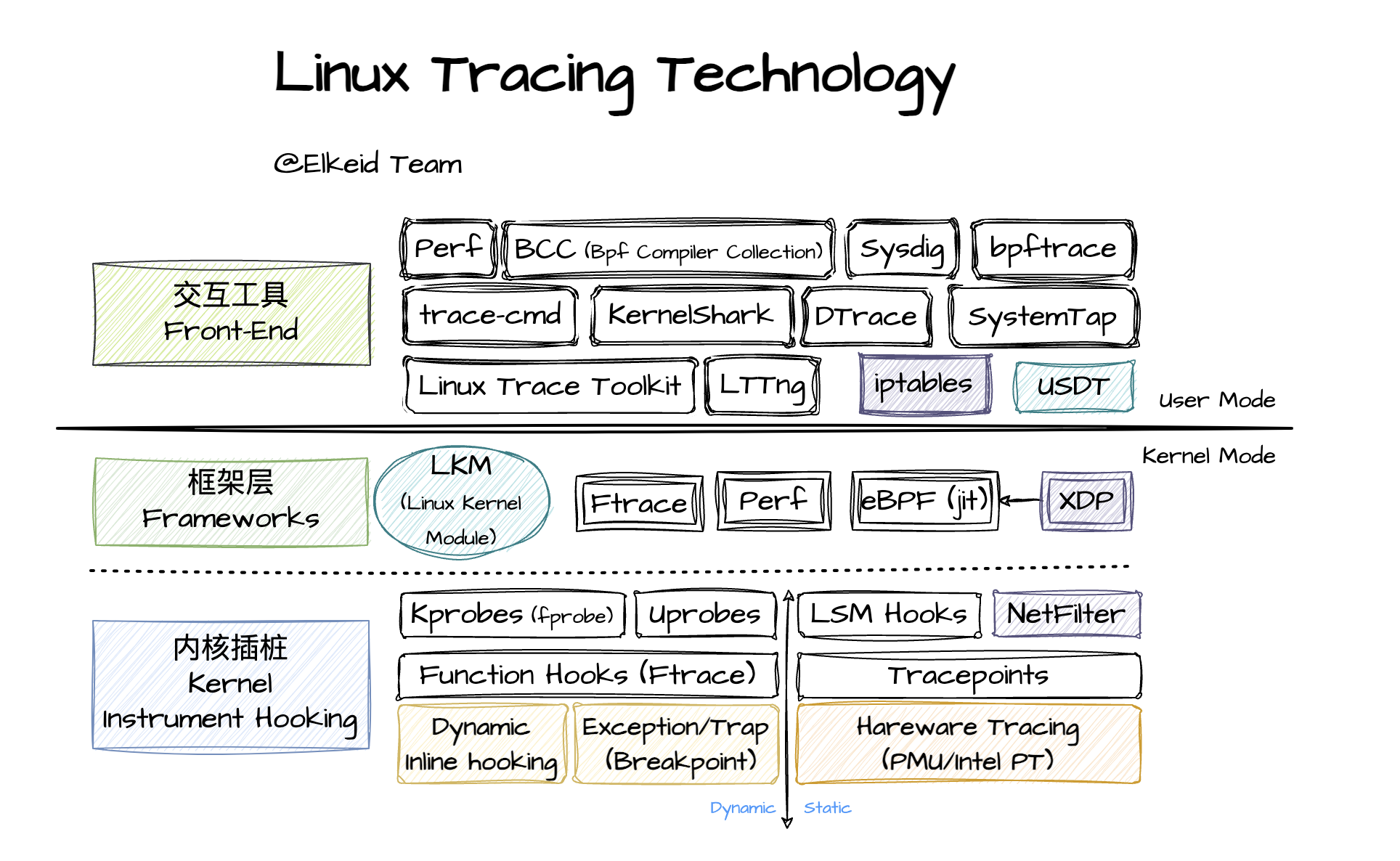
Linux系统上的所有追踪技术框架总的来说均可以拆分成三层:
1)最上层的交互工具层(Front-End):本层就是我们通常所说的Linux系统追踪技术这一概念,所代表的是动态追踪技术的用户层工具包,即直接与用户交互的追踪工具及追踪技术的展现层,如Perf工具、BCC工具包、SystemTap或tracecmd等;不同的工具会有不同的命令行约定及输出格式(不同的数据整合及展示方式)、与用户的交互方式等
2)最下层的内核插桩(Kernel Instrument Hooking):本层可以理解为Linux内核所提供的监控及跟踪能力,即动态追踪技术的基础架构(Infrastructure),是所有动态追踪技术框架的公共基础。此部分所限定的是数据的采集力(度度/种类、粒度)
3)中间框架层(Frameworks):本层可理解为接口层,即内核怎样使用和封装监控及跟踪能力并且以什么样的接口提供给应用层,主要作用就是承上启下,比如ftrace框架部分实现了ringbuffer来缓存事件日志并以tracefs形式将ftrace的监控能力直接暴露给用户程序。我们下面在详细各种跟踪框架时不就中间层做单独说明,而是放在交互工具及内核插桩部分中一起介绍。
3 前端交互工具
交互工具就是我们所平时直接使用的工具链,下面我们就分别介绍常用的追踪及性能工具,读者如果相了解各种工具的详细用法可参阅相关的参考资料。
3.1 perf
Perf工具正如其名称所示,其主要用于性能分析的场景,通过监控点数据采样的收集、处理及展示以定位热点(On-CPU)或冷点(Off-CPU),所以又被称作是Performance Counters for Linux (PCL)。
Perf提供了全栈采样和分析能力,无论用户进程还是操作系统内核均可以采集分析,此外亦能采集分析如CPU硬件事件,此部分主要利用了CPU的performance monitoring unit (PMU) 部件来采集如cache缓存的命中率/有效性或CPU微架构层面上流水线的利用率等CPU硬件统计数据。Perf常被称作是Linux系统上的瑞士军刀,可被用来进行单一应用层程序或操作系统内核的瓶颈分析与定位。Perf分析基于高频采样数据,因面会所引入不小的外部干扰(系统延时、I/O及CPU占用)。
下面的的例子是32位及64位MurMur Hash算法的性能摘要的对比测试:
root@devz1:/bd# perf stat ./MurMur32 testfile
Performance counter stats for './MurMur32 testfile':
6,201.00 msec task-clock # 1.000 CPUs utilized
54 context-switches # 8.708 /sec
0 cpu-migrations # 0.000 /sec
159,353 page-faults # 25.698 K/sec
17,940,754,358 cycles # 2.893 GHz
17,780,030,362 instructions # 0.99 insn per cycle
2,291,592,868 branches # 369.552 M/sec
17,469,263 branch-misses # 0.76% of all branches
6.202178179 seconds time elapsed
5.853408000 seconds user
0.348083000 seconds sys
root@devz1:/bd# perf stat ./MurMur64 testfile
Performance counter stats for './MurMur64 testfile':
6,195.04 msec task-clock # 1.000 CPUs utilized
39 context-switches # 6.295 /sec
3 cpu-migrations # 0.484 /sec
159,350 page-faults # 25.722 K/sec
17,923,596,344 cycles # 2.893 GHz
18,414,732,121 instructions # 1.03 insn per cycle
2,291,526,783 branches # 369.897 M/sec
17,442,514 branch-misses # 0.76% of all branches
6.195976210 seconds time elapsed
5.843555000 seconds user
0.351973000 seconds sys
下面的例子是用Perf来统计指定监控点mprotect系统调用在10秒内的调用次数,共测量了5次:
root@devz1:/bd# perf stat -a -I 10000 -e 'syscalls:*_mprotect'
# time counts unit events
10.001203375 2945573 syscalls:sys_enter_mprotect
10.001203375 2945678 syscalls:sys_exit_mprotect
10.001203375 0 syscalls:sys_enter_pkey_mprotect
10.001203375 0 syscalls:sys_exit_pkey_mprotect
20.003415918 2885202 syscalls:sys_enter_mprotect
20.003415918 2885113 syscalls:sys_exit_mprotect
20.003415918 0 syscalls:sys_enter_pkey_mprotect
20.003415918 0 syscalls:sys_exit_pkey_mprotect
30.004569553 2900982 syscalls:sys_enter_mprotect
30.004569553 2900982 syscalls:sys_exit_mprotect
30.004569553 0 syscalls:sys_enter_pkey_mprotect
30.004569553 0 syscalls:sys_exit_pkey_mprotect
40.005761270 3057035 syscalls:sys_enter_mprotect
40.005761270 3057036 syscalls:sys_exit_mprotect
40.005761270 0 syscalls:sys_enter_pkey_mprotect
40.005761270 0 syscalls:sys_exit_pkey_mprotect
50.006815036 3051245 syscalls:sys_enter_mprotect
50.006815036 3051246 syscalls:sys_exit_mprotect
50.006815036 0 syscalls:sys_enter_pkey_mprotect
50.006815036 0 syscalls:sys_exit_pkey_mprotect
用perf生成系统的整体性能分析报告:
root@devz1:/bd# perf record -a -g --call-graph dwarf -s
root@devz1:/bd# perf report -s symbol
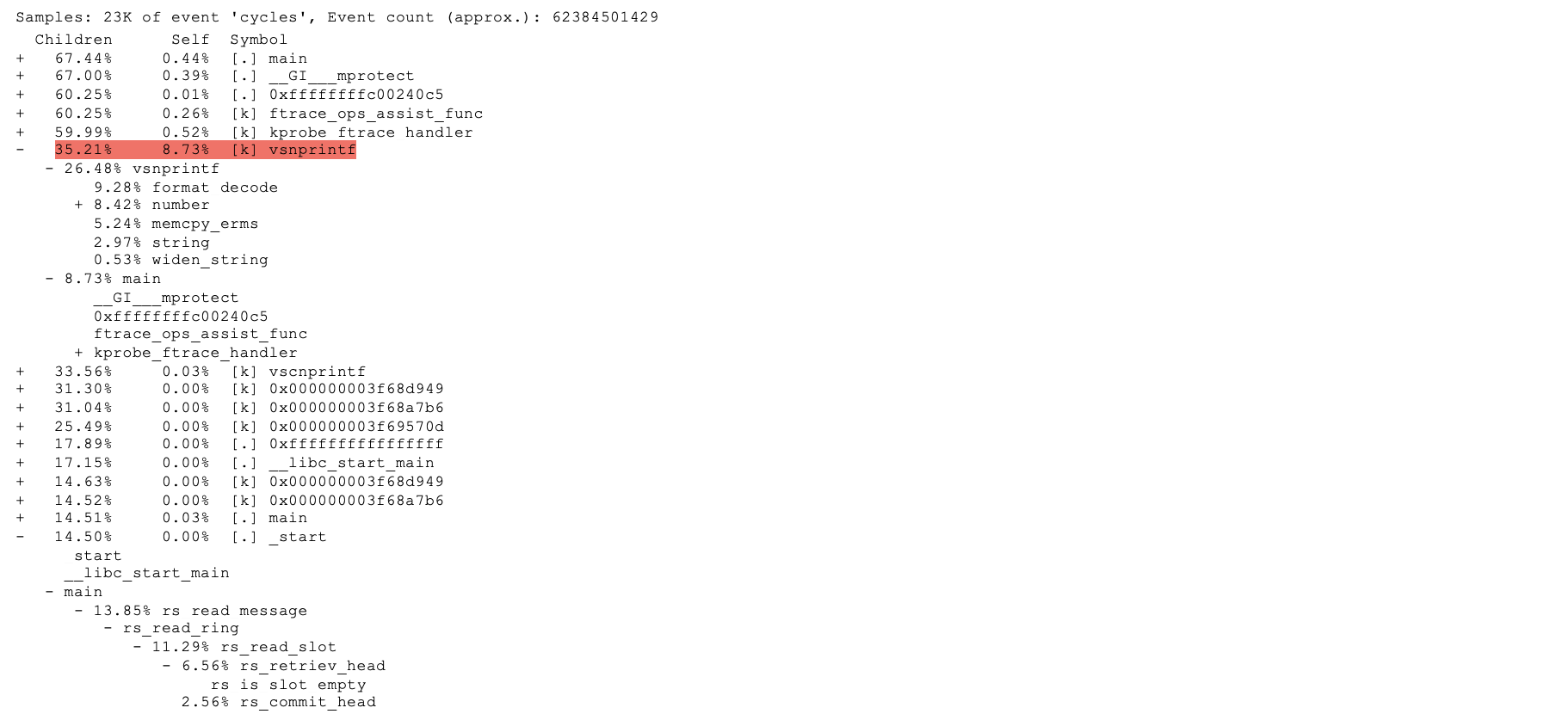
root@devz1:/bd# perf report -T

Perf最强大的一项可视化能力是以火焰图形式更直观地展示结果,如图所示:
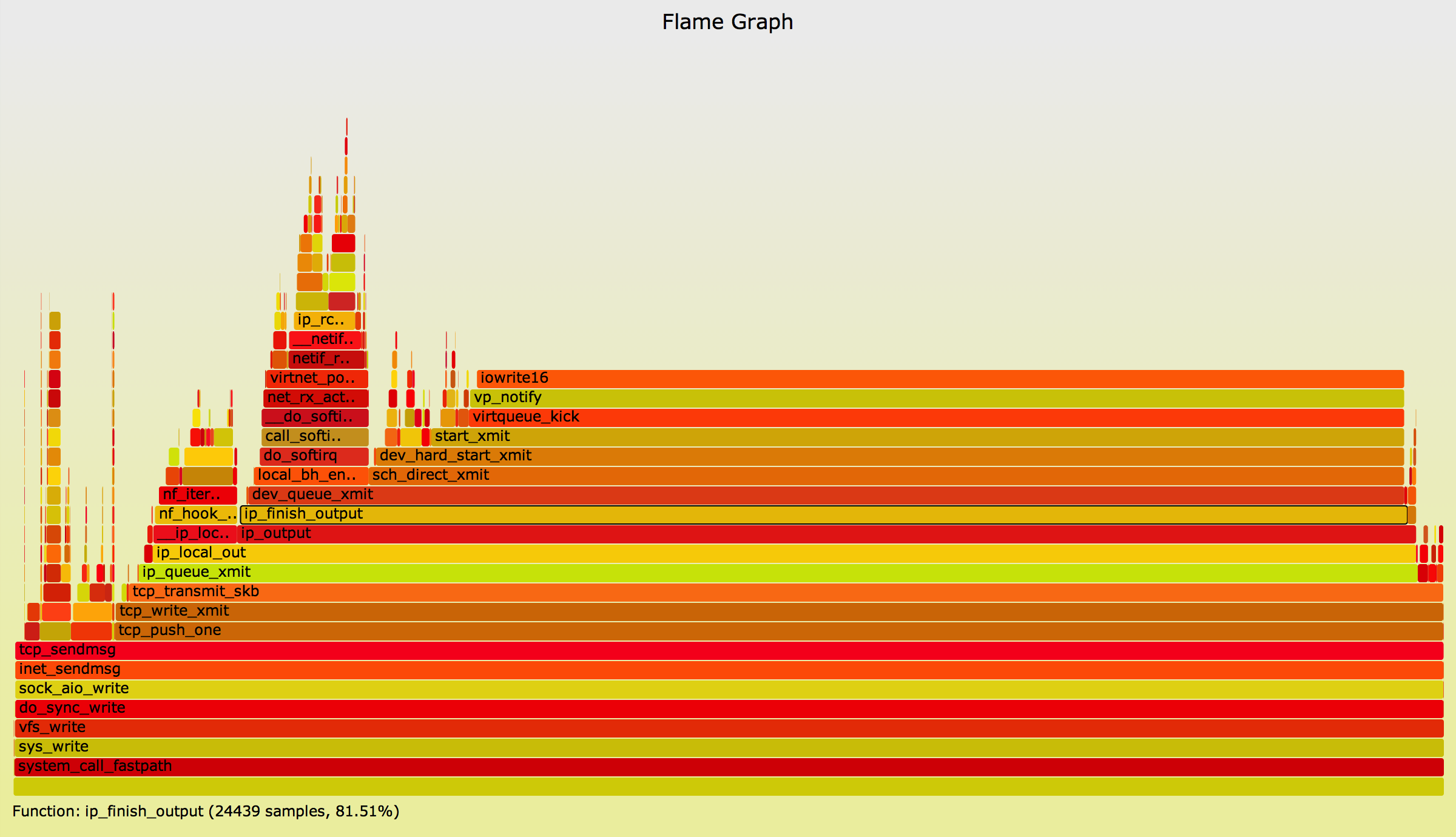
Perf工具支持所有2.6.31以来的内核版本,支持所有的常见发行版。在使用时需要注意与内核版本的匹配问题,最好使用内核自带的版本;另外Perf在处理及展示数据时(如函数名的提取等)需要相对应调试符号文件。
3.2 BCC & bpftrace
BCC ( Bpf Compiler Collectons) 既是eBPF程序的编写/编译框架,又是上百个测试、跟踪工具的合集,涵盖了Linux内核各个子系统。
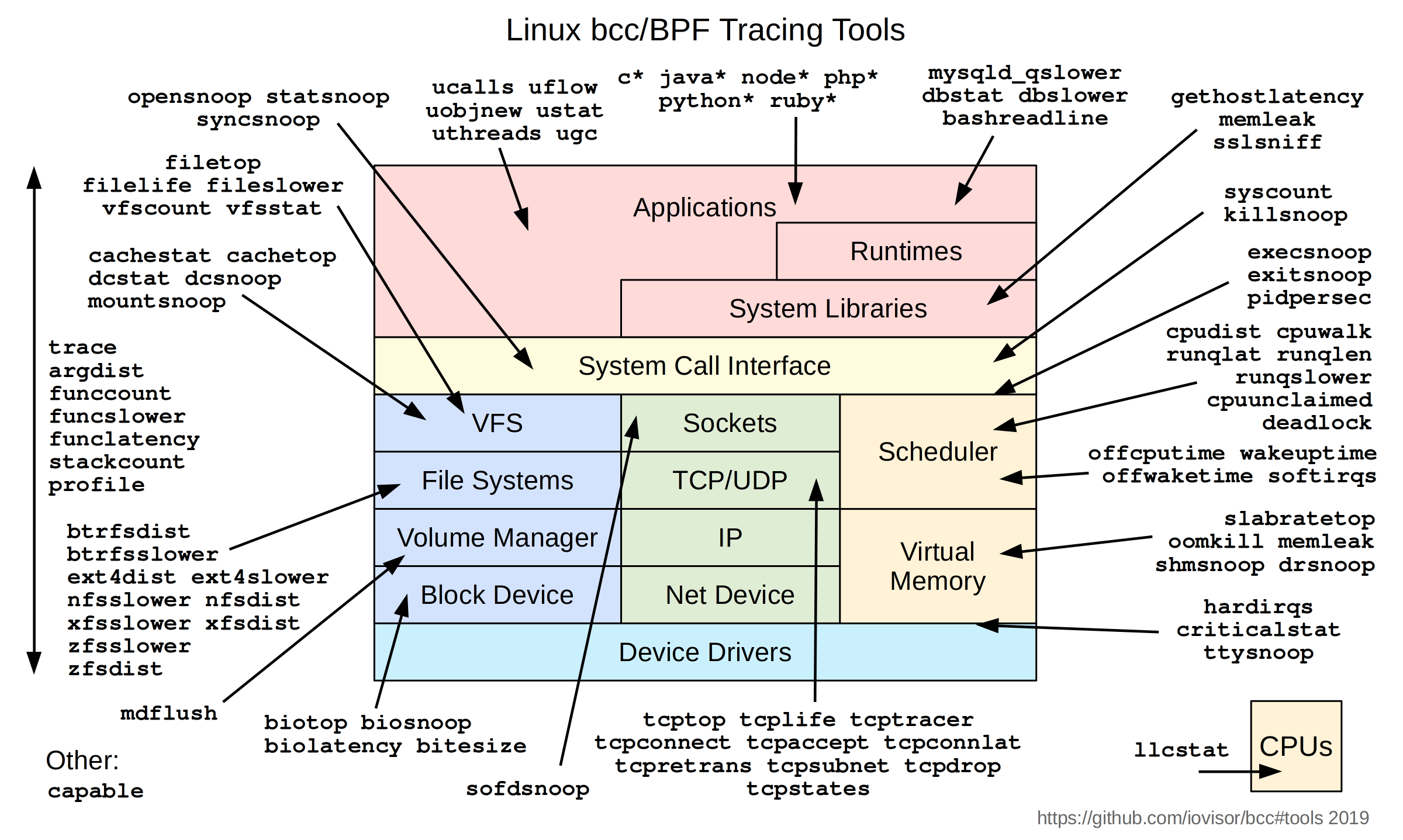
BCC是高度可定制的,支持以Python或LUA语言脚本并动态生成eBPF插桩程序,可充分利用eBPF的优势通过针对性的插桩以最小的CPU代价来获得更精准的监控数据。相较于Perf工具,主要差距在于通用性,对内核版本的要求较高,虽然eBPF所要求的最低内核版本是3.15,但大部BCC工具则需要4.1及之后的内核。
可参阅Brendan Gregg所著的《Systems Performance: Enterprise and the Cloud, 2e》或《BPF Performance Tools 》来了解性能分析的一般思路及BCC众多工具的用法。
与BCC工具相类似的是bpftrace工具,底层同样采用了eBPF,不同之处在于bpftrace实现了通过简单命令脚本实现了强大的eBPF的处理能力,在不少程度上可替代BCC工具链,可谓是调试及跟踪工具中的万能军刀。
3.3 Ftrace
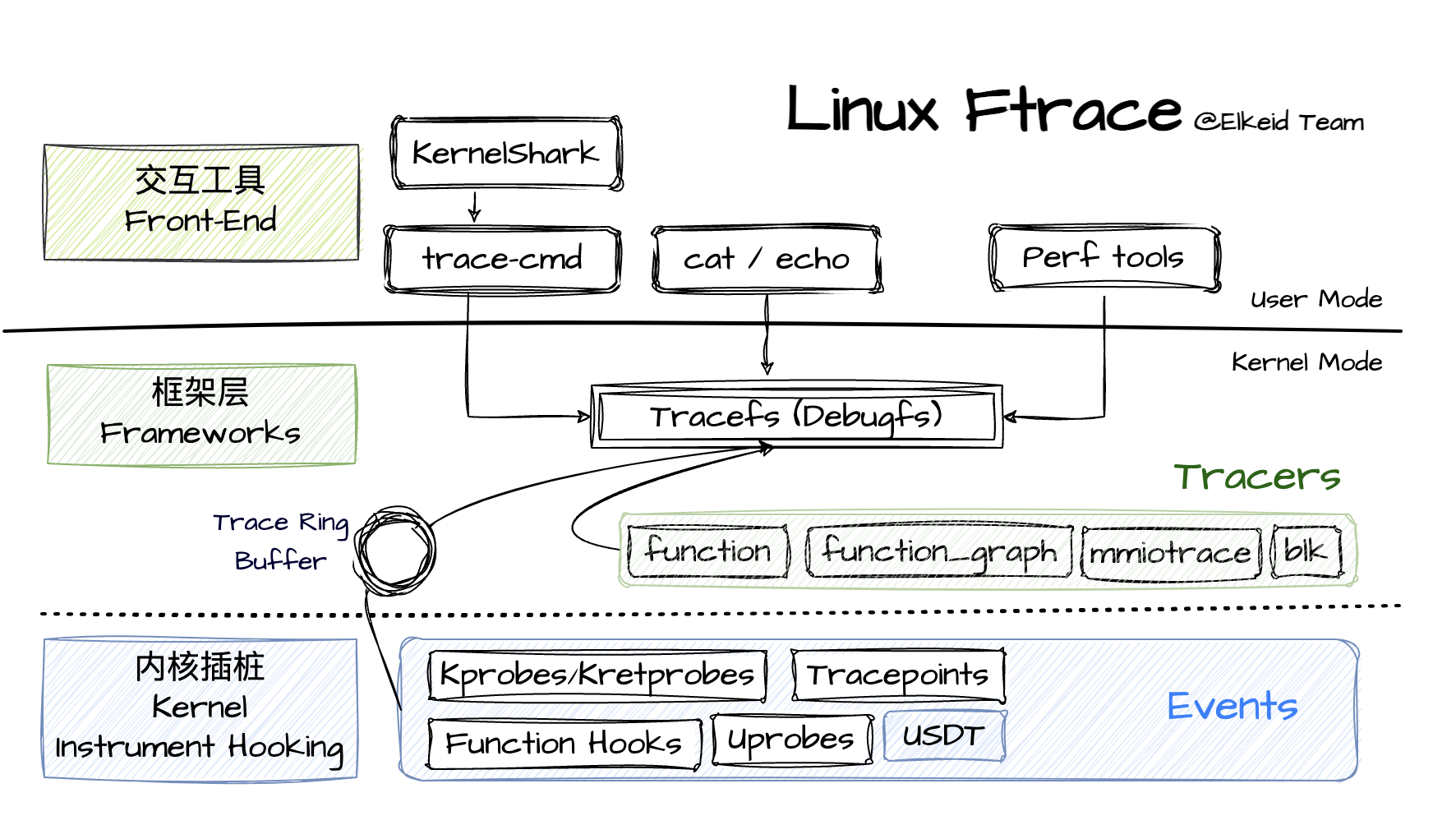
Ftrace是事实上的Linux默认内核跟踪框架,全称是function tracer,实际上包含了多个不同跟踪程序的框架,可以实现对内核函数整个调用栈的跟踪及执行流的时序分析。Ftrace跟踪框架既可以用前端工具如Trace-cmd或Trace Compass来收集处理跟踪事件,但也可以直接使用tracefs接口来进行交互 (注: 4.1之前的内核使用debugfs),后者使得ftrace可以很方便地应用在类似嵌入式系统这种受限场景中。
root@devz1:/bd/elkeid/driver/LKM# trace-cmd record -p function_graph -o prctl.cond.dat /bd/prctl.cond 1000
plugin 'function_graph'
CPU 0: 142884 events lost
CPU 1: 145553 events lost
CPU 2: 146946 events lost
CPU 3: 153171 events lost
CPU 4: 158666 events lost
CPU 5: 146837 events lost
CPU 6: 149830 events lost
CPU 7: 148248 events lost
CPU 8: 146777 events lost
CPU 9: 142771 events lost
CPU 10: 153487 events lost
CPU 11: 109054 events lost
CPU 12: 88133 events lost
CPU 13: 160568 events lost
CPU 14: 146435 events lost
CPU 15: 166039 events lost
CPU0 data recorded at offset=0x1ca000
677910 bytes in size (2805760 uncompressed)
CPU1 data recorded at offset=0x270000
662282 bytes in size (2760704 uncompressed)
CPU2 data recorded at offset=0x312000
671880 bytes in size (2826240 uncompressed)
CPU3 data recorded at offset=0x3b7000
666420 bytes in size (2760704 uncompressed)
CPU4 data recorded at offset=0x45a000
660560 bytes in size (2760704 uncompressed)
CPU5 data recorded at offset=0x4fc000
668253 bytes in size (2760704 uncompressed)
CPU6 data recorded at offset=0x5a0000
597882 bytes in size (2473984 uncompressed)
CPU7 data recorded at offset=0x632000
579340 bytes in size (2387968 uncompressed)
CPU8 data recorded at offset=0x6c0000
669085 bytes in size (2760704 uncompressed)
CPU9 data recorded at offset=0x764000
671154 bytes in size (2781184 uncompressed)
CPU10 data recorded at offset=0x808000
461914 bytes in size (2236416 uncompressed)
CPU11 data recorded at offset=0x879000
685712 bytes in size (2818048 uncompressed)
CPU12 data recorded at offset=0x921000
678074 bytes in size (2756608 uncompressed)
CPU13 data recorded at offset=0x9c7000
505564 bytes in size (2105344 uncompressed)
CPU14 data recorded at offset=0xa43000
664372 bytes in size (2785280 uncompressed)
CPU15 data recorded at offset=0xae6000
474461 bytes in size (1974272 uncompressed)
root@devz1:/bd/elkeid/driver/LKM# trace-cmd report -i prctl.cond.dat | head -n60
cpus=16
prctl-999-17870 [010] 106972.553766: funcgraph_entry: 0.663 us | mutex_unlock();
prctl-999-17870 [010] 106972.553767: funcgraph_entry: 0.171 us | preempt_count_add();
prctl-999-17870 [010] 106972.553767: funcgraph_entry: 0.128 us | preempt_count_sub();
prctl-999-17870 [010] 106972.553768: funcgraph_entry: | __f_unlock_pos() {
prctl-999-17870 [010] 106972.553768: funcgraph_entry: 0.133 us | mutex_unlock();
prctl-999-17870 [010] 106972.553768: funcgraph_exit: 0.375 us | }
prctl-999-17870 [010] 106972.553768: funcgraph_entry: 0.132 us | syscall_exit_to_user_mode_prepare();
prctl-999-17870 [010] 106972.553768: funcgraph_entry: | exit_to_user_mode_prepare() {
prctl-999-17870 [010] 106972.553769: funcgraph_entry: 0.145 us | fpregs_assert_state_consistent();
prctl-999-17870 [010] 106972.553769: funcgraph_exit: 0.429 us | }
prctl-999-17870 [010] 106972.553770: funcgraph_entry: | __x64_sys_execve() {
prctl-999-17870 [010] 106972.553770: funcgraph_entry: | kprobe_ftrace_handler() {
prctl-999-17870 [010] 106972.553771: funcgraph_entry: 0.347 us | get_kprobe();
prctl-999-17870 [010] 106972.553771: funcgraph_entry: | pre_handler_kretprobe() {
prctl-999-17870 [010] 106972.553772: funcgraph_entry: | execve_entry_handler() {
prctl-999-17870 [010] 106972.553772: funcgraph_entry: | get_execve_data() {
prctl-999-17870 [010] 106972.553772: funcgraph_entry: | count() {
prctl-999-17870 [010] 106972.553772: funcgraph_entry: 0.172 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553773: funcgraph_entry: 0.157 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553773: funcgraph_entry: 0.161 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553773: funcgraph_entry: 0.155 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553774: funcgraph_entry: 0.155 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553774: funcgraph_entry: 0.154 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553774: funcgraph_entry: 0.152 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553774: funcgraph_entry: 0.156 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553775: funcgraph_entry: 0.154 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553775: funcgraph_entry: 0.154 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553775: funcgraph_entry: 0.156 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553775: funcgraph_entry: 0.151 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553776: funcgraph_entry: 0.155 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553776: funcgraph_entry: 0.154 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553776: funcgraph_entry: 0.152 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553777: funcgraph_entry: 0.155 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553777: funcgraph_entry: 0.153 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553777: funcgraph_entry: 0.151 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553777: funcgraph_entry: 0.168 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553778: funcgraph_entry: 0.154 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553778: funcgraph_entry: 0.153 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553778: funcgraph_entry: 0.153 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553778: funcgraph_entry: 0.152 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553779: funcgraph_entry: 0.149 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553779: funcgraph_entry: 0.155 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553779: funcgraph_entry: 0.149 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553779: funcgraph_entry: 0.158 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553780: funcgraph_exit: 7.694 us | }
prctl-999-17870 [010] 106972.553780: funcgraph_entry: | count() {
prctl-999-17870 [010] 106972.553780: funcgraph_entry: 0.154 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553780: funcgraph_entry: 0.154 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553781: funcgraph_entry: 0.152 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553781: funcgraph_exit: 0.960 us | }
prctl-999-17870 [010] 106972.553781: funcgraph_entry: | __kmalloc() {
prctl-999-17870 [010] 106972.553781: funcgraph_entry: 0.150 us | kmalloc_slab();
prctl-999-17870 [010] 106972.553781: funcgraph_entry: | __kmem_cache_alloc_node() {
prctl-999-17870 [010] 106972.553781: funcgraph_entry: 0.131 us | should_failslab();
prctl-999-17870 [010] 106972.553782: funcgraph_exit: 0.588 us | }
prctl-999-17870 [010] 106972.553782: funcgraph_exit: 1.140 us | }
prctl-999-17870 [010] 106972.553782: funcgraph_entry: 0.154 us | get_user_arg_ptr();
prctl-999-17870 [010] 106972.553783: funcgraph_entry: | __check_object_size() {
prctl-999-17870 [010] 106972.553783: funcgraph_entry: 0.127 us | check_stack_object();
另外值得一提的是,KernelShark是Perf的数据展示的GUI版本,能以图形的方式多样展示数据:
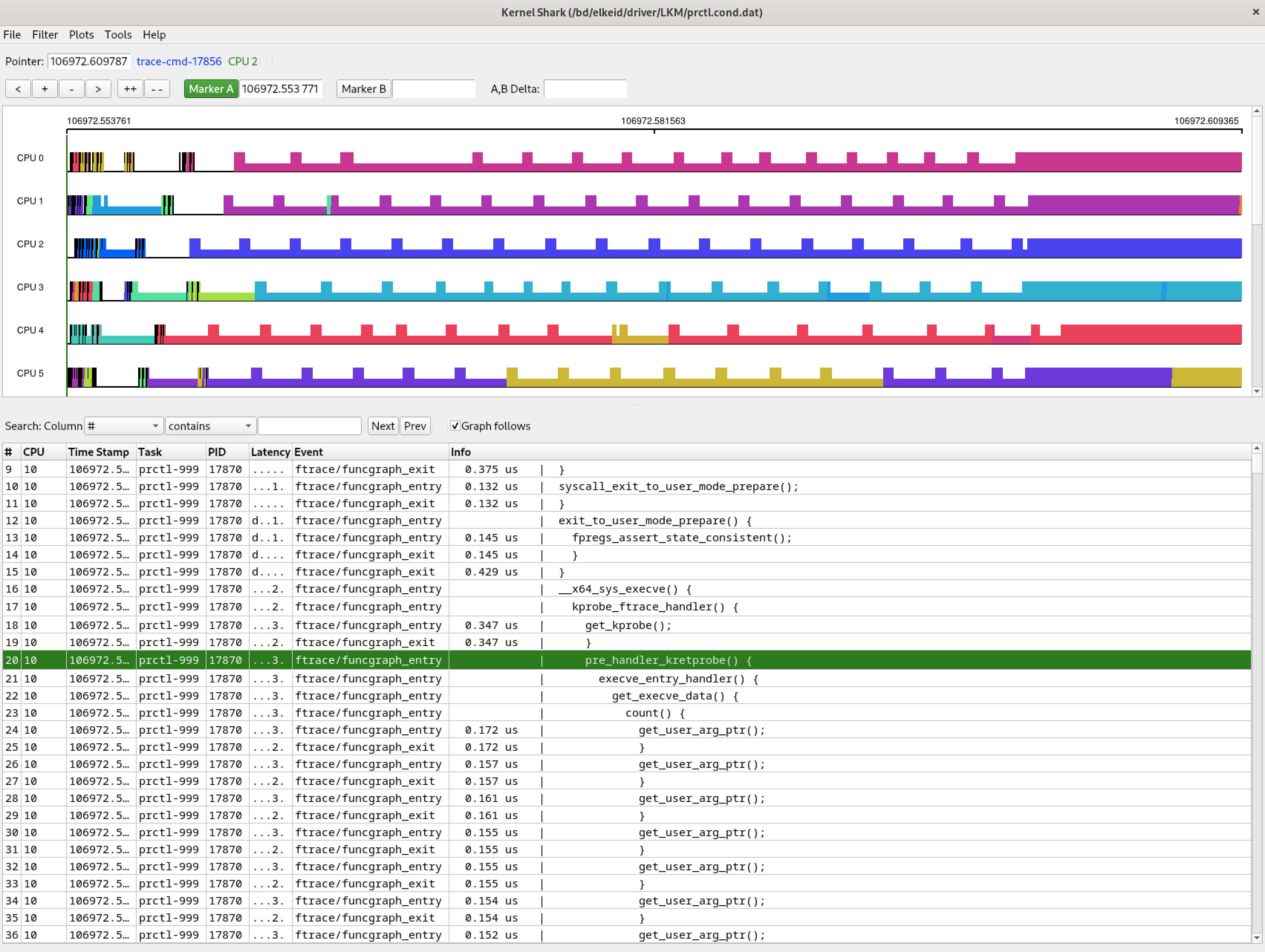
3.4 SystemTap
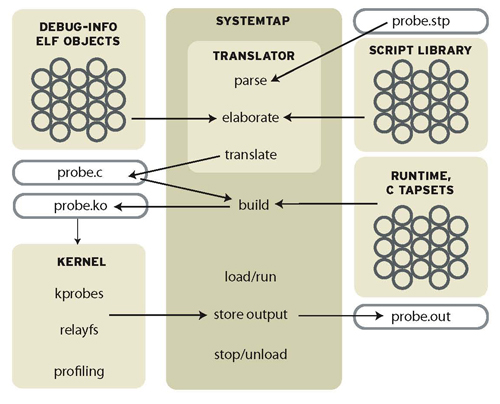
SystemTap是Redhat的DTrace方案,是RHEL、Fedora等红帽系发行般的默认追踪技术框架。2003年Solaris DTrace横空出世,席卷整个Linux开发世界,引起了广泛且持久的关注,彼时Linux的内核跟踪能力还没有建立起完整的生态,而RedHat的答案就是SystemTap,并维护至今,虽然没有集成至内核,但对主流发行版的支持一直都有很好的贯彻,如Debian、SLES等。
SystemTap实现了自己的脚本语言,以对应DTrace的D语言,SystemTap对LKM的编程框架进行了二次封装,实现了脚本至C代码的即时转换,最终通过动态编译并加载内核模块(LKM实现了针对相应关注点的监控能力。所以SystemTap需要额外的依赖:如内核头文件、编译链支持以及调试符号信息等。
下面的例子是使用SystemTap监控libc malloc函数的调用 :
[root@CentOS8 ~]# cat malloc.stp
probe process("/lib64/libc.so.6").function("malloc") {
printf("malloc called: process: %s\n", execname());
print_ubacktrace();
}
[root@C82 ~]# stap malloc.stp
malloc called: process: in:imjournal
0x7fd360fc0a90 : __libc_malloc+0x0/0x300 [/usr/lib64/libc-2.28.so]
malloc called: process: tuned
0x7efd845f1a90 : __libc_malloc+0x0/0x300 [/usr/lib64/libc-2.28.so]
malloc called: process: tuned
...
SystemTap会自动加载一个临时模块,可通过lsmod来查询:
[root@C82 matt]# lsmod | grep stap
stap_038834a35c414369cc17bce6916b3411_1641 757760 0
[root@C82 ~]# ls -l /tmp
total 8
drwx------. 2 root root 4096 Jul 20 17:45 stap7X8kn4
...
[root@C82 ~]# ls /tmp/stap7X8kn4/
stap_038834a35c414369cc17bce6916b3411_1641.ko stap_038834a35c414369cc17bce6916b3411_1641_src.c
3.5 LTTng
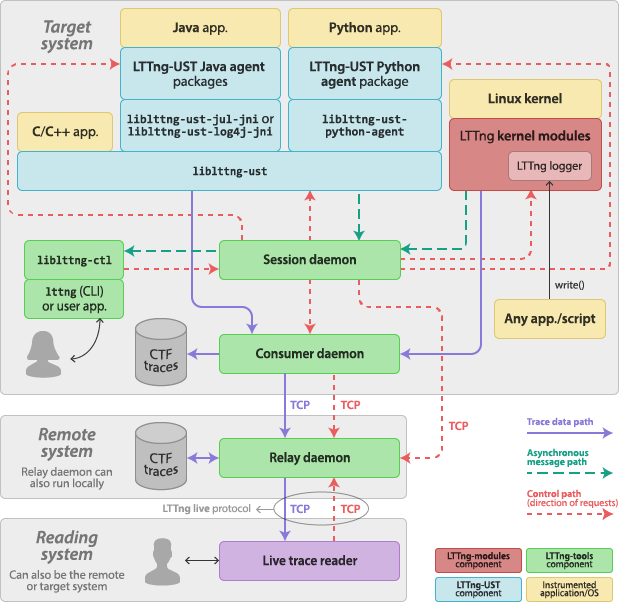
Linux Trace Toolkit Next Generation (LTTng)于2005年发布,只看名称的话很容易被人理解为LTT (Linux Trace Toolkit) 的升级版本,但实际上是Mathieu Desnoyers对LTT的完全重写。LTTng虽然没能整合进Linux内核主干版本,但Linux tracepoints的开发及性能优化均有Mathieu及LTTng项目的功劳,而tracepoints则是perf及ftrace框架的重要支撑,是Linux跟踪框架的起步。
LTTng项目一直在维护状态,并且增加了对USDT的支持以收集用户态进程自定义监控点数据。在结果分析及展示上可用TraceCompass工具进行辅助。
3.6 Sysdig
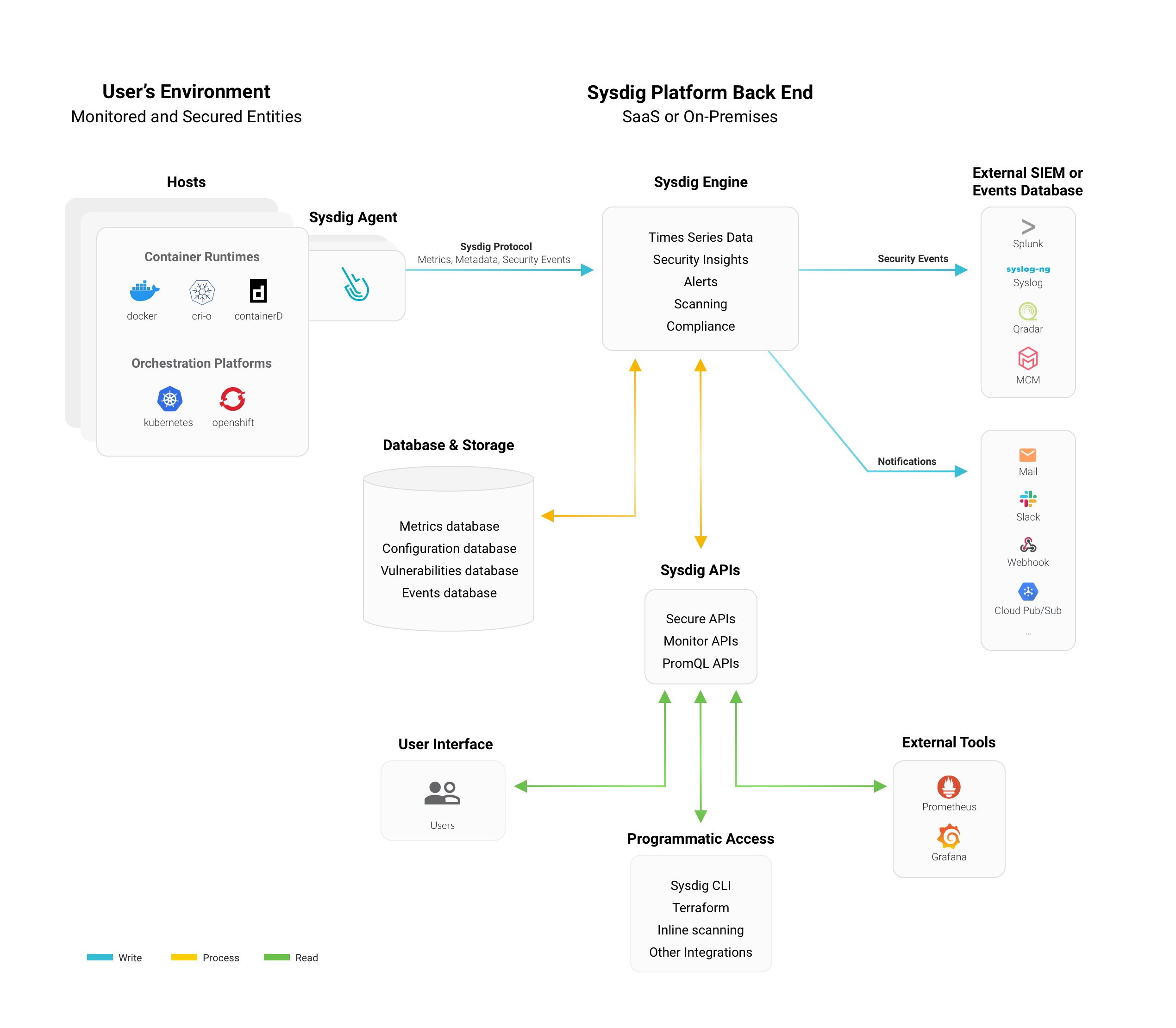
Sysdig是一种Linux环境的可视化工具,功能上可以理解为strace + tcpdump + htop + iftop + lsof等工具的集合。Sysdig发布之初主要是用于提升Linux系统可观察性,后续又加入了针对容器本地监控以侧重云环境下的行为监控,Sysdig支持lua脚本。
3.7 Oracle DTrace
Oracle Linux Dtrace是 Solaris DTrace的移植版本,由Oracle发起并维护,主要用在Oracle Linux发行版上。与SystemTap一样,DTrace也是以内核模块为载体来提供内核运行时态的探测能力。与Oracle DTrace类似的项目dtrace4linux,则是由 Paul D. Fox个人所开发和维护的移植版本,可参见[DT04: dtrace4linux @ github],两个项目其实是各自独立的。DTrace源生于Solairs (由Sun Microsystems inc开发,后Sun公司被Oracle收购),Sun公司曾以CDDL协议开源整个Solaris操作系统,但Linux内核是基于GPLv2的,也正因为两种协议的差异使得源生于Solaris OS的很多诱人的功能如DTrace、ZFS等不能直接并入Linux内核,这也是DTrace for Linux仅支持Oracle Linux系统的主要原因,相对于日新月异的Linux内核来说DTrace移植开发的节奏要慢很多。
DTrace的强大之处是D语言的脚本支持能力,用户可以自定义D语言程序来达成对系统软硬件运行时态的探测。以【LT04: Linux Performance Analysis Tools】其中的一个例子来介绍Dtrace的使用,此例子统计了sshd进程的所有tcp_sendmsg()调用的size参数并以分布直方图形式展示给用户:
# dtrace -n 'fbt::tcp_sendmsg:entry /execname == "sshd"/ {
@["bytes"] = quantize(arg3); }'
dtrace: description 'fbt::tcp_sendmsg:entry ' matched 1 probe
^C
bytes
value ------------- Distribution ------------- count
16 | 0
32 |@@@@@@@@@@@@@@@@ 1869
64 |@@@@@@@@@@@@@ 1490
128 |@@@ 355
256 |@@@@ 461
512 |@@@ 373
1024 |@ 95
2048 | 4
4096 | 1
8192 | 0
3.8 Linux Audit
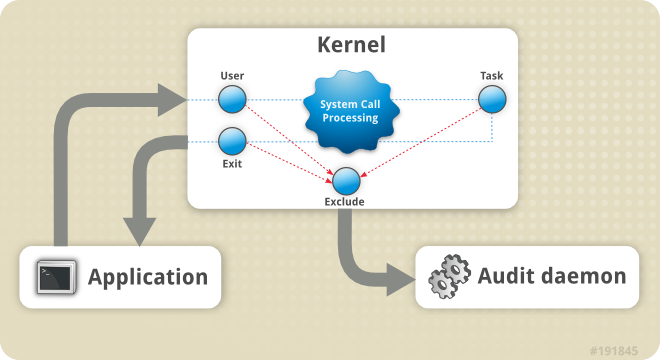
Linux Audit是一个用于监控和记录Linux系统相关活动的安全框架,可以追踪系统中的安全相关事件,如用户登录、文件访问、系统调用等等。Audit提供了强大且灵活的安全审计机制,几乎无所不能,无论是监控系统活动,还是合规确保,或者威胁发现等场景均适用,并且能根据系统的安全需求和政策要求进行灵活配置。
Audit是一个完整的审计系统解决方案,自身形成了一个完整的闭环生态,故可定制性上缺乏灵活性,另外所被诟病比较多的则是性能问题,就因为其监控控制的粒度问题。
Linux内核监控点由Audit子系统来实现,均为显式的静态调用,自2.6内核以来就已经存在,所以每个监控点的功能亦是静态的,并且为了性能及稳定性等因素,每条日志的输出基本限定于相关操作函数的调用参数,没有可扩展或自定义的空间。应用层服务进程Auditd与内核kaudit通过netlink机制通信,所有的内核日志只能由Auditd来消费。目前也有新的开源应用层框架替代如go-audit。
4 插桩机制
程序或操作系统本身对用户来说就是一个二进制的黑箱,当评估其内部运作逻辑是否与设计相符、以及调研错误来源或性能热点时,我们就不得不利用插桩技术来进行探测其内部的执行流程及状态数据。这里所说的插桩其实就是常说的instrumenting 及 hooking两个概念,二者的含义基本一致,只不过前者更侧重于数据收集而不改变其行为序列,而后者更侧重于改变或替代原执行流程。
最常用的插桩机制是Inline hooking,目前依然被广泛使用,此技术通过动态修改代码指令以执行监控代码然后再返回原执行流程。Linux内核本身提供了kprobe、uprobe及ftarce等插桩技术框架,其实也是对inline hooking的封装并提供了一致性的内核支持函数,用以掩盖对不同指令架构及不同内核版本的处理。
4.1 插桩机制汇总
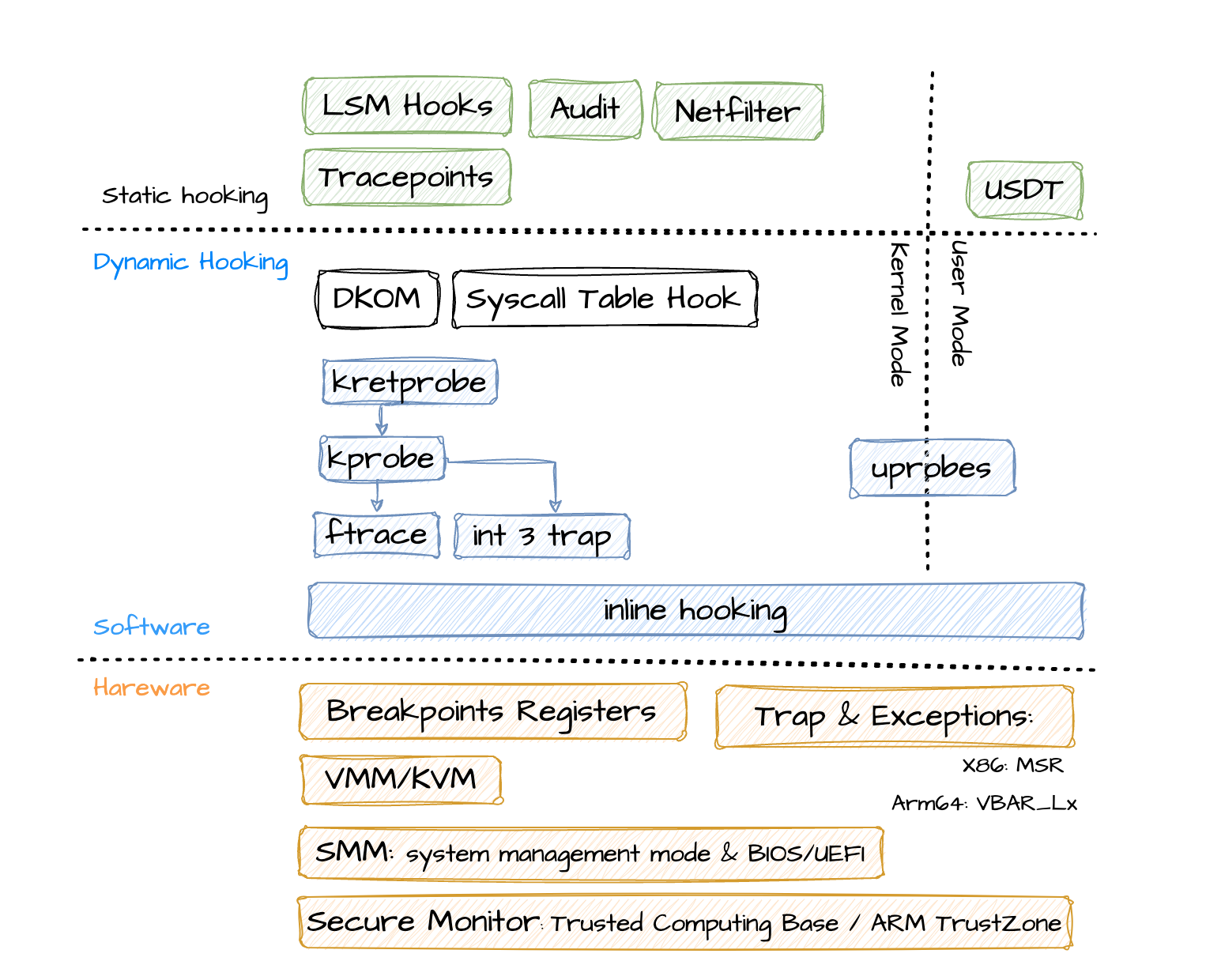
插桩机制可分类的维度有很多,从使用范围上可分内核态及用户态,从实现机制上可分顾静态及动态插桩机制,总的来说可归纳为以下几类:
4.1.1通用插桩机制
- inline hook机制:即直接修改指令的方式
4.1.2 内核插桩机制
静态插桩机制:
- Tracepoints:内核自定义了近2000多个静态监控点,可监控内核及intree模块的内部运作
- LSM HOOK:主要适用于安全模块,如SELinux/AppArmor等,能够中断及阻止当前操作
- Audit:用于Linux Audit系统,已内置于内核,可根据需要输出相应监控点功子系统的日志
- NetFilter:监控网络数据包,防火墙、隧道、VPN等均可基于Netfilter框架来实现
动态插桩机制:
- ftrace:kernel function hook的插桩机制
- kprobes/uprobes:内核的动态插桩框架,基于int 3 trap及ftace实现
- Linux内核通知链(CPU、Mount, USB等):Linux内核向模块提供的事件通知机制,模块可以注册回调
自定义内核插桩机制:
- Syscall table hook:直接修改syscall table以指向自己的程序代码
- DKOM (operations table hook):内核是以文件来管理所有资源的,每种资源如文件均有相应的回调接口,实际上可以理解为一组函数指针,通过修改这些指针的指向从而可以劫持对此类型所有或单个对象的操作
- 中断向量hook:中断向量表的入口,CPU通过寄存器保存了不同中断的入口地址以实现中断处理的硬件加速
- 硬件调试断点:调试断点支持指令断点及内存访问断点,但是不同的架构、CPU类型所提供的调试寄存器数量不同,一般都比较少
- 高精度软/硬中断:中断机制主要用于采样,同样也能用于hook的场景,但对性能影响较大,并且不能确保中断点的指令位置
4.1.3 用户态插桩机制
- USDT:User Statically Defined Trace,即用户层的Tracepoint,需要程序在编写时显示定义的监控点,如libc、mysql等应用均有支持
- uprobes: 用户态的动态跟踪机制,其实现及回调处理均是在内核中处理的。原理上其实是用breakpoint改写用户态指令的方式触发异常并跳转至内核态的处理程序。自3.5并入的内核,但3.14之后才提供了较好的可用性,tracefs及perf等框架均可以直接使用uprobes
- LD_PRELOAD: 利用Linux .so共享库的搜索路径使得加载器优先绑定指定共享库的导出函数,从而跳过默认共享库的绑定,可实现函数级的hook
- GOT/PLT表hook:利用ELF/COFF文件的导入及导出表来进行函数级的hook
4.2 通用inline hooking
Inline-hooking是最常用的一种插桩技术,无论是安全软件还是恶意软件都有广泛使用,特别是Windows平台,inline hooking的使用非常频繁,几乎所有的安全软件均依赖于此技术来监控应用层的恶意行为。
Inline-hooking技术简单来就是直接修改代码指令改变原指令的执行流程转而执行我们的监控代码,等监控代码执行完成后再返回至原路径继续执行,最常用的方法就是将函数入口处的指令修改成跳转 (JMP )指令。
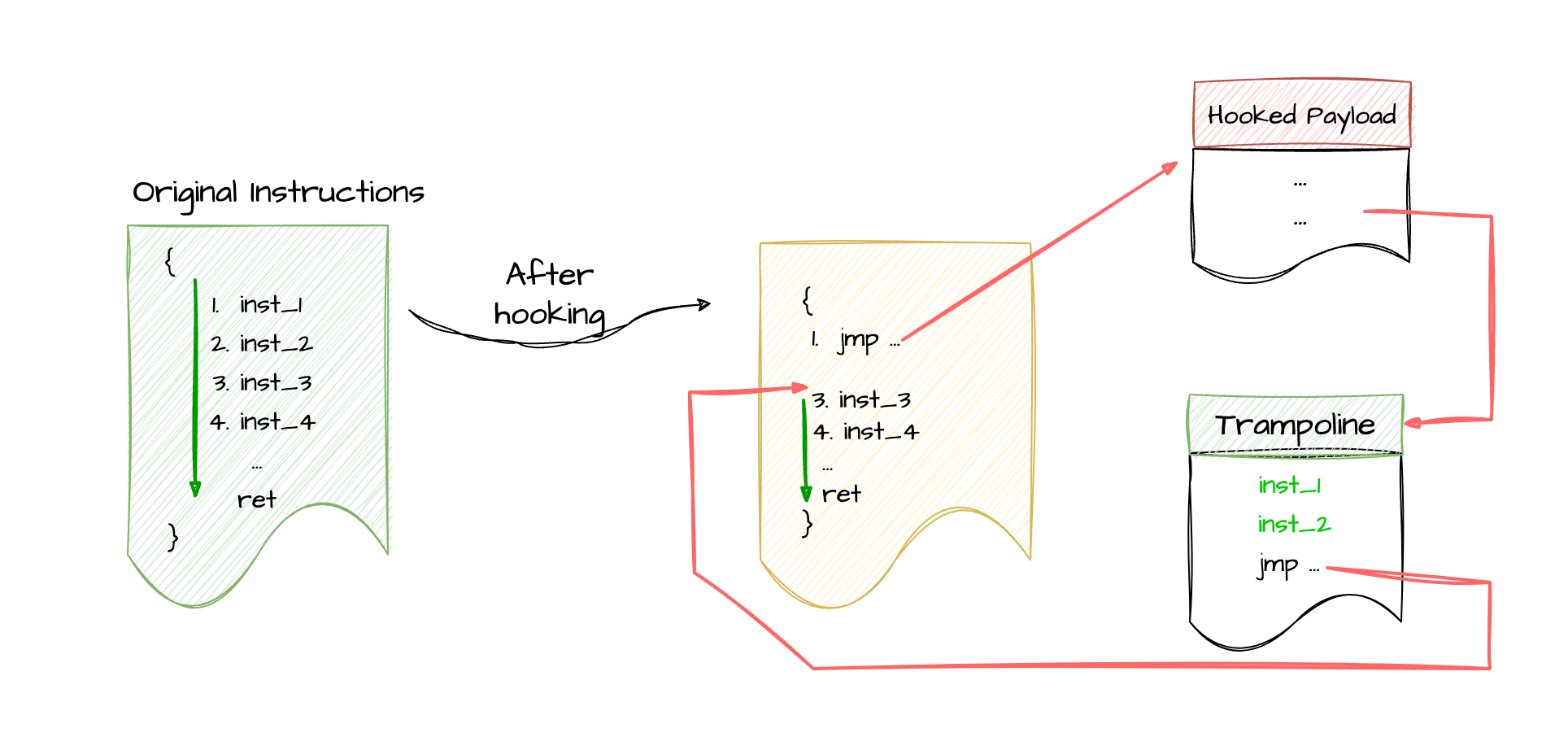
很多rootkit程序如reptile为了达成更好的藏匿效果就使用了inline hooking,syscall table hook方式使用频率很高,很多安全软件均有针对syscall table的审计和校验。下面以reptile为例来说明,
vfs_read内核函数被劫持前的代码:
pwndbg> x/100i 0xffffffff9980b900
0xffffffff9980b900: nop DWORD PTR [rax+rax*1+0x0
0xffffffff9980b905: push r14
0xffffffff9980b907: push r13
0xffffffff9980b909: push r12
0xffffffff9980b90b: push rbp
0xffffffff9980b90c: push rbx
0xffffffff9980b90d: mov eax,DWORD PTR [rdi+0x44]
0xffffffff9980b910: test al,0x1
0xffffffff9980b912: je 0xffffffff9980ba1b
...
加载reptile之后,vfs_read被篡改了,直接跳转至地0xffffffffc03013f0:
pwndbg> x/100i 0xffffffff9980b900
0xffffffff9980b900: jmp 0xffffffffc03013f0
0xffffffff9980b905: push r14
0xffffffff9980b907: push r13
0xffffffff9980b909: push r12
0xffffffff9980b90b: push rbp
0xffffffff9980b90c: push rbx
0xffffffff9980b90d: mov eax,DWORD PTR [rdi+0x44]
0xffffffff9980b910: test al,0x1
0xffffffff9980b912: je 0xffffffff9980ba1b
...
沿此被修改后的代码流程,可最终找到存放原vfs_read函数指令的跳板,即0xffffffffc03013d0:
pwndbg> x/100i 0xffffffffc03013f0
0xffffffffc03013f0: lock inc DWORD PTR [rip+0xffffffffffffffc9] # 0xffffffffc03013c0
0xffffffffc03013f7: sub rsp,0x40
0xffffffffc03013fb: mov rax,QWORD PTR [rsp+0x48]
0xffffffffc0301400: mov QWORD PTR [rsp],rax
0xffffffffc0301404: mov rax,QWORD PTR [rsp+0x50]
0xffffffffc0301409: mov QWORD PTR [rsp+0x8],rax
0xffffffffc030140e: mov rax,QWORD PTR [rsp+0x58]
0xffffffffc0301413: mov QWORD PTR [rsp+0x10],rax
0xffffffffc0301418: mov rax,QWORD PTR [rsp+0x60]
0xffffffffc030141d: mov QWORD PTR [rsp+0x18],rax
0xffffffffc0301422: mov rax,QWORD PTR [rsp+0x68]
0xffffffffc0301427: mov QWORD PTR [rsp+0x20],rax
0xffffffffc030142c: mov rax,QWORD PTR [rsp+0x70]
0xffffffffc0301431: mov QWORD PTR [rsp+0x28],rax
0xffffffffc0301436: mov rax,QWORD PTR [rsp+0x78]
0xffffffffc030143b: mov QWORD PTR [rsp+0x30],rax
0xffffffffc0301440: mov rax,QWORD PTR [rsp+0x80]
0xffffffffc0301448: mov QWORD PTR [rsp+0x38],rax
0xffffffffc030144d: movabs rax,0xffffffffc0694830
0xffffffffc0301457: call rax
0xffffffffc0301459: add rsp,0x40
0xffffffffc030145d: lock dec DWORD PTR [rip+0xffffffffffffff5c] # 0xffffffffc03013c0
0xffffffffc0301464: ret
pwndbg> x/100i 0xffffffffc0694830
0xffffffffc0694830: push rbp
0xffffffffc0694831: mov DWORD PTR [rip+0x2f4d],0x1 # 0xffffffffc0697788
0xffffffffc069483b: mov rbp,rsi
0xffffffffc069483e: push rbx
0xffffffffc069483f: mov rax,QWORD PTR [rip+0x28ca] # 0xffffffffc0697110
0xffffffffc0694846: call 0xffffffff99c20750
0xffffffffc069484b: mov rbx,rax
0xffffffffc069484e: mov eax,DWORD PTR [rip+0x2f30] # 0xffffffffc0697784
0xffffffffc0694854: test eax,eax
0xffffffffc0694856: jne 0xffffffffc0694868
0xffffffffc0694858: mov rax,rbx
0xffffffffc069485b: mov DWORD PTR [rip+0x2f23],0x0 # 0xffffffffc0697788
0xffffffffc0694865: pop rbx
0xffffffffc0694866: pop rbp
0xffffffffc0694867: ret
...
pwndbg> x /10i 0xffffffff99c20750
0xffffffff99c20750: jmp rax
pwndbg> x/60i 0xffffffffc03013d0
0xffffffffc03013d0: nop DWORD PTR [rax+rax*1+0x0]
0xffffffffc03013d5: jmp 0xffffffff9980b905
通常的热补丁技术也使用inline hook,不过热补丁的使用相对更简单一些,因为要修改的指令位置是精心选择的,并且只有完整性核验通过的情况下才会进行热补操作,而一个通用的inline hooking引擎则需要处理更多的问题。
- 内存不可写的问题:此部分需要修改页面属性或通过页面重新映射来达成,X86体系CPU提供了WP位可以强制改写内存,但此方式下的修改不会触发COW (copy-on-write),针对用户层的共享代码(如libc共享库)的改写要特别注意
- 跳板指令生成的问题:以X86指令体系为例,JMP跳转指令的总长度为5个字节,即1个字节的操作数 (0xE9) 及 4个字节的相对地址的偏移。对原始函数的入口写入一个跳转指令会覆盖至少5个字节,而这5个字节可能是多打指令,其中也可能有短跳转指令,所以一般hook框架都需要集成一个反汇编引擎,并且不同的CPU框架需要使用不同指令集的汇编引擎,像ARM及RISC-V一类RISC体系相对更简单一些。跳板指令生成的另一个问题是位置选择,如X86指令JMP的操作数即4个字节的相对地址偏移是个有符号数,即只能跳转相对当前位置上下各2G的空间,如果超出这个范围的话就需要增加中间跳板或改成绝对地址跳转, X86_64绝对跳转指令总长度为12-14字节。
- 指令撕裂问题:当改写多条指令时就会遇到正好有CPU执行中间指令的情况,特别是多CPU环境中正好线程执行在这几条指令中间的可能性大大增加,一旦遇到此情况将最终导致程序或系统崩溃。针对运行时态的操作系统内核或应用程序可通过暂停其它CPU或当前进程的其它线程以降低指令撕裂发生的概率,但并不能从根本上杜绝。当然如果是在应用程序在加载执行的初始化阶段的话,可有效避免。针对此情况下的应对就是只改写一条指令,因为指令的执行对CPU来说是原子性的,不管CPU的微架构或流水线有多复杂,指令执行的原子性是CPU必须保证的。针对X86指令来说将入口代码的第一个字节修改为0xCC,即 int 3 trap指令,然后通过捕获及并修复继续执行位置的方式来达成改变原执行流程的目的,这也是Linux uprobe所使用的技术方案,此方案的不便之处就是需要内核的协助,即int3 trap异常处理函数要正确识别此uprobe监控点。kprobe的最早实现也是基于int3 trap的,后来的版本则基于ftrace,ftrace则是需要编译器的支持才行,后面再介绍ftace机制时再做详述。
Inline hooking这种技术的明显限制是针对同一个函数的多次hook问题,主要的困扰在于卸载时的跳板无法安全清理的问题,最终结果将导致跳板数量的累加。此外inline hooking的插桩行为改变了指令序列,相关的安全审计软件或者可信计算系统在进行完整性校验时将会发现这种不一致性。另外在使能Intel CPU shadow stack安全技术的系统上也会有兼容性问题。
Linux系统下很少有较成熟的inline hook框架,但Windows系统上有着众多成熟框架,如detours,EasyHook、mhook等。
4.3 Tracepoints
Linux内核预置了近2000个tracepoints,使用tracepoints来监控非常容易,并且支持监控点的批量处理,并且每一个tracepoint都有自己独立的开关,以最小化在监控点未使用的情况下的性能消耗,其中内核使用了jump label、static call等技术,有兴趣的不妨进一步延伸阅读相关资料。
Tracepoints监控点不仅覆盖了用户进程所有的系统调用,也囊括了内核各个关键子系统内部的整个执行过程。总体上Linux内核的tracepoints可以分为以下几类:
- 进程和线程跟踪点:这些tracepoints与进程和线程的创建、调度、结束等操作有关。通过跟踪这些tracepoints,可以了解进程和线程的执行情况,帮助我们分析和优化多任务系统的性能和行为。
- 内核事件和操作跟踪点:这些tracepoints与内核内部的事件和操作有关,如内存分配、锁操作、调度器操作等。通过跟踪这些tracepoints,可以深入了解内核的内部工作机制和性能特征。
- 安全和错误跟踪点:这些tracepoints用于跟踪安全相关的事件和错误条件。例如,可以跟踪系统调用的安全性检查、文件访问权限错误等。安全和错误跟踪点可以帮助我们监视和调试系统的安全性和错误处理。
- 内核子系统跟踪点:这些tracepoints与内核的不同子系统相关,例如文件系统、网络、内存管理等。它们提供了一种跟踪和调试内核子系统行为的方式,可以用于监视和分析特定子系统的性能和行为。
- 硬件事件跟踪点:这些tracepoints与硬件相关的事件和操作有关。例如,可以跟踪CPU的中断、缓存事件、DMA操作等。硬件事件跟踪点可以帮助我们深入了解硬件的行为和性能瓶颈。
Tracepoints覆盖了所有syscall的调用、任务调度与切换、硬件等,几乎涵盖了所有的系统事件,当然不同的内核版本会有差异,针对内核v6.1的统计信息如下,基于perf list的输出(等同于 /sys/kernel/debug/tracing/events):
| 项目 |
数量 |
| syscall raw (sys_enter/sys_exit) |
2 |
| syscalls(sys_enter_xxx/sys_exit_xxx) |
690 |
| sched及task相关事件: 调度层监控点 |
29 |
| cgroup事件 |
13 |
| module事件:涉及模块的加载、卸载、引用等 |
5 |
| net事件:协议及封包相关事件 |
16 |
| kvm事件 |
91 |
| 所有tracepoints |
1944 |
Tracepoint的支持默认是打开的,相关内核选项为CONFIG_TRACEPOINTS及CONFIG_HAVE_SYSCALL_TRACEPOINTS,当然不排除第三方自定义内核关闭tracepoints的情况。
另外还需要注意的是tracepoints在不同的内核版本上有较大差异,使用时需要做进一步甄别,特别是老版本内核的系统,如CentOS 6系统等。另外还有些个别性的缺陷问题,如sched:process_exec这个监控点的支持是人Linux 3.4才开始有的;ARM64架构上syscall execve及execveat的处理上也有问题,在新进程加载成功的情况下没有syscall exit回调,此问题在5.20及之后的内核版本才得到修复。
用户在自己的模块中也可以显示地定义自己的Tracepoint,这样就可以直接利用Trace-cmd或perf工具来直接跟踪与分析自己的模块。
4.4 Ftrace
在Section 3.3中我们介绍了Ftrace是Linux内核动态跟踪技术的基准框架,在这里我们重点介绍Ftrace的动态插桩机制。Ftrace实现了内核”任意函数点“插桩的能力,并且可以输出调用参数、内部变量,甚至改变函数执行流程、返回值等。
Ftrace的”任意函数点“插桩能力实际上是由在内核编译阶段由gcc编译器完成的,在开启CONFIG_FTRACE的情况下,会打开内核编译开关 -pg,此参数会在函数头添加一个跳板函数的调用 :call _mcount或fentry调用指令。即使mcount函数定义为空,此举会带来可达13%的性能损失。
为了解决性能损失的问题,内核引入了CONFIG_DYNAMIC_FTRACE选项,此选项会在内核启动时将所有的跳板函数的调用指令改写成no指令 (nop DWORD PTR [rax+rax*1+0x0])。当注册新的ftrace监控点时,ftrace框架会动态修改相应函数的跳板调用指令,以下面的例子来说明:
do_init_module函数在vmlinux内核镜像文件中的代码如下:
pwndbg> disass do_init_module
Dump of assembler code for function do_init_module:
Address range 0xffffffff81151a50 to 0xffffffff81151c5d:
0xffffffff81151a50 <+0>: call 0xffffffff81079320 <__fentry__>
0xffffffff81151a55 <+5>: push rbp
0xffffffff81151a56 <+6>: mov edx,0x10
0xffffffff81151a5b <+11>: mov esi,0xcc0
0xffffffff81151a60 <+16>: mov rbp,rsp
0xffffffff81151a63 <+19>: push r14
0xffffffff81151a65 <+21>: push r13
0xffffffff81151a67 <+23>: push r12
0xffffffff81151a69 <+25>: mov r12,rdi
0xffffffff81151a6c <+28>: mov rdi,QWORD PTR [rip+0x156480d] # <kmalloc_caches+32>
0xffffffff81151a73 <+35>: call 0xffffffff812cbc10 <kmalloc_trace>
0xffffffff81151a78 <+40>: test rax,rax
0xffffffff81151a7b <+43>: je 0xffffffff81151c55 <do_init_module+517>
0xffffffff81151a81 <+49>: mov r13,rax
...
我们可以看到call 0xffffffff81079320 <__fentry__>这条指令实际上非由源代码生成,而是gcc在编译时自动添加的。在系统启动之后,我们用调试器来观察运行时态的内核代码,可以看出第一条指令已被修改:
pwndbg> disass do_init_module
0xffffffff81151a50 <+0>: nop DWORD PTR [rax+rax*1+0x0]
0xffffffff81151a55 <+5>: push rbp
0xffffffff81151a56 <+6>: mov edx,0x10
0xffffffff81151a5b <+11>: mov esi,0xcc0
0xffffffff81151a60 <+16>: mov rbp,rsp
0xffffffff81151a63 <+19>: push r14
0xffffffff81151a65 <+21>: push r13
0xffffffff81151a67 <+23>: push r12
0xffffffff81151a69 <+25>: mov r12,rdi
0xffffffff81151a6c <+28>: mov rdi,QWORD PTR [rip+0x156480d] # <kmalloc_caches+32>
0xffffffff81151a73 <+35>: call 0xffffffff812cbc10 <kmalloc_trace>
0xffffffff81151a78 <+40>: test rax,rax
0xffffffff81151a7b <+43>: je 0xffffffff81151c55 <do_init_module+517>
0xffffffff81151a81 <+49>: mov r13,rax
...
然后我们注册一个do_init_mdoule的kprobe hook,再来观察存在ftrace hook的情况下do_init_module的入口指令:
pwndbg> disass do_init_module
0xffffffff81151a50 <+0>: call 0xffffffffc0206000
0xffffffff81151a55 <+5>: push rbp
0xffffffff81151a56 <+6>: mov edx,0x10
0xffffffff81151a5b <+11>: mov esi,0xcc0
0xffffffff81151a60 <+16>: mov rbp,rsp
0xffffffff81151a63 <+19>: push r14
0xffffffff81151a65 <+21>: push r13
0xffffffff81151a67 <+23>: push r12
0xffffffff81151a69 <+25>: mov r12,rdi
0xffffffff81151a6c <+28>: mov rdi,QWORD PTR [rip+0x156480d] # <kmalloc_caches+32>
0xffffffff81151a73 <+35>: call 0xffffffff812cbc10 <kmalloc_trace>
0xffffffff81151a78 <+40>: test rax,rax
0xffffffff81151a7b <+43>: je 0xffffffff81151c55 <do_init_module+517>
0xffffffff81151a81 <+49>: mov r13,rax
...
0xffffffffc0206000就是kprobe的跳板代码,其主要作用就是调用kprobe_ftrace_handler以处理kprobe回调或进行kretprobe回调的堆栈hook,当然还需要进行现场 (寄存器等context相关变量) 的保存与恢复:
pwndbg> x/100i 0xffffffffc0206000
0xffffffffc0206000: pushf
0xffffffffc0206001: push rbp
0xffffffffc0206002: push QWORD PTR [rsp+0x18]
0xffffffffc0206006: push rbp
0xffffffffc0206007: mov rbp,rsp
0xffffffffc020600a: push QWORD PTR [rsp+0x20]
0xffffffffc020600e: push rbp
0xffffffffc020600f: mov rbp,rsp
0xffffffffc0206012: sub rsp,0xa8
0xffffffffc0206019: mov QWORD PTR [rsp+0x50],rax
0xffffffffc020601e: mov QWORD PTR [rsp+0x58],rcx
......
0xffffffffc02060cd: mov QWORD PTR [rsp+0x98],rcx
0xffffffffc02060d5: lea rbp,[rsp+0x1]
0xffffffffc02060da: lea rcx,[rsp]
0xffffffffc02060de: call 0xffffffff8107e500 <kprobe_ftrace_handler>
0xffffffffc02060e3: mov rax,QWORD PTR [rsp+0x90]
......
0xffffffffc020615a: add rsp,0xd0
0xffffffffc0206161: popf
0xffffffffc0206162: ret
Ftrace支持同一个监控点的多次hook,如不同的模块同时监控了同一个内核函数,ftrace hook框架已经封装了相关的处理。另外Dynamic Ftrace在修改跳板调用指令时也考虑到了指令撕裂问题,可参见文档【FT01 】 以了解详情。
4.5 Kprobes
Krobes(Kernel Probes)允许在内核运行时(即不需要重新编译内核或模块)动态地插入断点和探测点。最新的Kprobes是基于ftrace的,之前的版本是利用了int 3 trap指令来达成的对目标函数的监控。Kprobes共有3种类型,包括Kprobe、Jprobe和Kretprobe:
- Kprobe:Kprobe是一种基本的探测点,用于在内核函数的任意指令位置插入断点。当断点被触发时,Kprobe会执行一个预先注册的处理程序(handler)。处理程序可以访问和修改寄存器、内存和堆栈等数据,以实现对内核操作的监控和修改。
- Kretprobe:Kretprobe本身就是架构在Kprobe之上的,Kretprobe需要在Kprobe触发时通过额外的堆栈hook以使能完成回调在在函数返回时被触发。Kretprobe可以在函数返回时获取返回值和堆栈信息,以实现对内核函数执行结果的监控和分析。AMD64架构上针对尾调用做了性能上的优化,即通过JMP跳转的方式以减少函数调用的层数,同时遐免了函数调用的额外压栈及返回时的取栈动作,此举会影响kretprobe hook的使用。
- Jprobe,可以当作是特殊的Kprobe。Kprobe通过修改函数入口指令监控函数调用的入口,而Jprobe允许在函数中间直接中断并查看参数及局部变量,这使得Jprobe更适合用于分析和调试内核函数的行为,但同时也会带来不可控问题,直接导致Jprobe被从主线内核中移除,具体可参见:https://lwn.net/Articles/735667/ & https://lkml.org/lkml/2017/10/2/386。
Kprobes可以理解成对Ftrace的封装,增加了函数参数的处理,同时增加了函数返回回调的功能,即Kretprobe,但Kretprobe在可扩展性上有较大性能问题,所以在性能敏感或高频次调用的热点函数上尽量避免或者进行动态的开启及关闭,当然开启及关闭的的动作同样也会引入新的问题,如为了处理指令撕裂问题需要暂停其它CPU的执行等。
4.6 LSM hook
Linux Security Module(LSM)Hooking机制是Linux内核中的一个安全框架,允许多个安全模块(如SELinux、AppArmor、Landlock等)在内核中插入钩子(Hooks),以实施特定的安全策略和访问控制。LSM Hooking机制的设计目的是提供一种模块化、可扩展的安全解决方案,使得内核可以灵活地支持不同的安全模型和需求。
每个LSM组件可根据自己的需求填充security_operations的回调结构,这些函数指针代表了各种内核操作(如文件访问、进程创建等)的安全钩子。通过在这些钩子函数中插入特定的安全模块,LSM可以对内核操作实施访问控制和审计等功能
LSM hook最早由SELinux使用并引入内核,本就是为安全而生的,安全软件所主要关注的进程、程序/动态库/模块加载、内存及文件等高危操作与Linux LSM的监控点亦基本符合,LSM hook本身也提供了操作阻止功能,是安全组件及HIPS (Host-based Intrusion Prevention System) 产品的最佳选择。
最新的6.4内核共提供了多达247个监控回调,之前的内核版本会少一些,如5.4.2内核所支持的回调数量为216,二者数量上相差31,所以在使用中要注意不同内核版本上所支持的回调种类上的差异:
| 类别 |
钩子函数个数 |
功能 |
| ptrace |
2 |
ptrace操作的权限检查 |
| 能力机制 |
3 |
Capabilities相关操作的权限检查 |
| 磁盘配额 |
2 |
配盘配额管理操作的权限检查 |
| 超级块 |
15 |
mount/umount/文件系统/超级块相关操作的权限检查 |
| dentry |
2 |
dentry相关操作的权限检查 |
| 文件路径 |
12 |
文件名/路径相关操作的权限检查 |
| inode |
37 |
inode相关操作的权限检查 |
| file |
12 |
file相关操作的权限检查 |
| 程序加载 |
5 |
运行程序时的权限检查 |
| 进程 |
20 |
线程/进程相关操作的权限检查 |
| IPC |
15 |
IPC消息/共享内存/信号量等操作的权限检查 |
| 网络 |
38 |
网络相关操作的权限检查: socket/tun/sctp等操作 |
| XFRM |
11 |
IPSec/XFRM相关操作的权限检查 |
| 密钥 |
4 |
密钥管理相关操作的权限检查 |
| 审计 |
4 |
内核审计相关操作的权限检查 |
| Binder |
4 |
Android IPC子系统相关操作的权限检查 |
| Perf |
5 |
perf工具相关操作 |
| iouring |
3 |
i/o uring相关 |
| eBPF |
7 |
eBPF系统调用及相关操作 |
| ... |
|
|
| 总计 |
247 |
|
LSM虽然全称是Linux Secuirty Module,但其并不是真正的Linux内核模块(LKM),而是必须编译在内核镜像中,即in-tree模式。与其它的功能类似,不同的内核版本间差异也比较大,其中3个影响较大的版本改变:
1) < 4.2.0
只允许一个模块注册,security_ops 指针指向此模块的 security_operations
2)>= 4.2.0
允许多个模块注册,通过双向链表(security_hook_heads)管理(struct list_head)
3) >= 4.17.0
允许多个模块注册,通过单链表(security_hook_heads)管理 (struct hlist_head)
LSM hooks虽然是HIPS产品在监控机制上的最佳选择,但对于Linux模块来说却非常不好即,比如自4.12.0开始,security_hook_heads列表在内核初始化之后将不可写,当然有其它方式可达成改写目的,不过更大的障碍还在于security_hook_heads不再导出,这样的话只能通过分析函数指令来定位此链表头,以security_inode_create为例:
pwndbg> disass security_inode_create
Dump of assembler code for function security_inode_create:
0xffffffff8152d3b0 <+0>: nop DWORD PTR [rax+rax*1+0x0]
0xffffffff8152d3b5 <+5>: test BYTE PTR [rdi+0xd],0x2
0xffffffff8152d3b9 <+9>: jne 0xffffffff8152d407 <security_inode_create+87>
0xffffffff8152d3bb <+11>: push rbp
0xffffffff8152d3bc <+12>: mov rbp,rsp
0xffffffff8152d3bf <+15>: push r14
0xffffffff8152d3c1 <+17>: mov r14,QWORD PTR [rip+0x1189610] # 0xffffffff826b69d8 <security_hook_heads+440>
0xffffffff8152d3c8 <+24>: push r13
0xffffffff8152d3ca <+26>: push r12
0xffffffff8152d3cc <+28>: push rbx
0xffffffff8152d3cd <+29>: test r14,r14
0xffffffff8152d3d0 <+32>: je 0xffffffff8152d3f8 <security_inode_create+72>
0xffffffff8152d3d2 <+34>: mov r12,rdi
0xffffffff8152d3d5 <+37>: mov r13,rsi
0xffffffff8152d3d8 <+40>: movzx ebx,dx
0xffffffff8152d3db <+43>: mov rax,QWORD PTR [r14+0x18]
0xffffffff8152d3df <+47>: mov edx,ebx
0xffffffff8152d3e1 <+49>: mov rsi,r13
0xffffffff8152d3e4 <+52>: mov rdi,r12
0xffffffff8152d3e7 <+55>: call rax
0xffffffff8152d3e9 <+57>: nop DWORD PTR [rax]
0xffffffff8152d3ec <+60>: test eax,eax
0xffffffff8152d3ee <+62>: jne 0xffffffff8152d3fa <security_inode_create+74>
0xffffffff8152d3f0 <+64>: mov r14,QWORD PTR [r14]
0xffffffff8152d3f3 <+67>: test r14,r14
0xffffffff8152d3f6 <+70>: jne 0xffffffff8152d3db <security_inode_create+43>
0xffffffff8152d3f8 <+72>: xor eax,eax
0xffffffff8152d3fa <+74>: pop rbx
0xffffffff8152d3fb <+75>: pop r12
0xffffffff8152d3fd <+77>: pop r13
0xffffffff8152d3ff <+79>: pop r14
0xffffffff8152d401 <+81>: pop rbp
0xffffffff8152d402 <+82>: ret
0xffffffff8152d403 <+83>: int3
0xffffffff8152d404 <+84>: int3
0xffffffff8152d405 <+85>: int3
0xffffffff8152d406 <+86>: int3
0xffffffff8152d407 <+87>: xor eax,eax
0xffffffff8152d409 <+89>: ret
0xffffffff8152d40a <+90>: int3
0xffffffff8152d40b <+91>: int3
0xffffffff8152d40c <+92>: int3
0xffffffff8152d40d <+93>: int3
End of assembler dump.
pwndbg>
从0xffffffff8152d3c1处的指令即可算出inode_create的链表头为0xffffffff826b69d8。遗憾的是不同的内核版本、及不同的体系架构均会生成不同的指令组合,所要面临的情况比此示例要复杂的多。
值得庆幸的是5.7之后的内核 eBPF框架已支持LSM Hooks,我们可以编写eBPF程序来直接挂接LSM Hooks,以file_mprotect为例:
SEC("lsm/file_mprotect")
int BPF_PROG(mprotect_audit, struct vm_area_struct *vma,
unsigned long reqprot, unsigned long prot, int ret)
{
/* ret is the return value from the previous BPF program
* or 0 if it's the first hook.
*/
if (ret != 0)
return ret;
int is_heap;
is_heap = (vma->vm_start >= vma->vm_mm->start_brk &&
vma->vm_end <= vma->vm_mm->brk);
/* Return an -EPERM or write information to the perf events buffer
* for auditing
*/
if (is_heap)
return -EPERM;
}
要注意的一点是虽然5.7及之内的内核已经支持LSM Hooks,但不一定会打开相应的配置选项:CONFIG_BPF_LSM,使用前必须确认。
4.7 eBPF
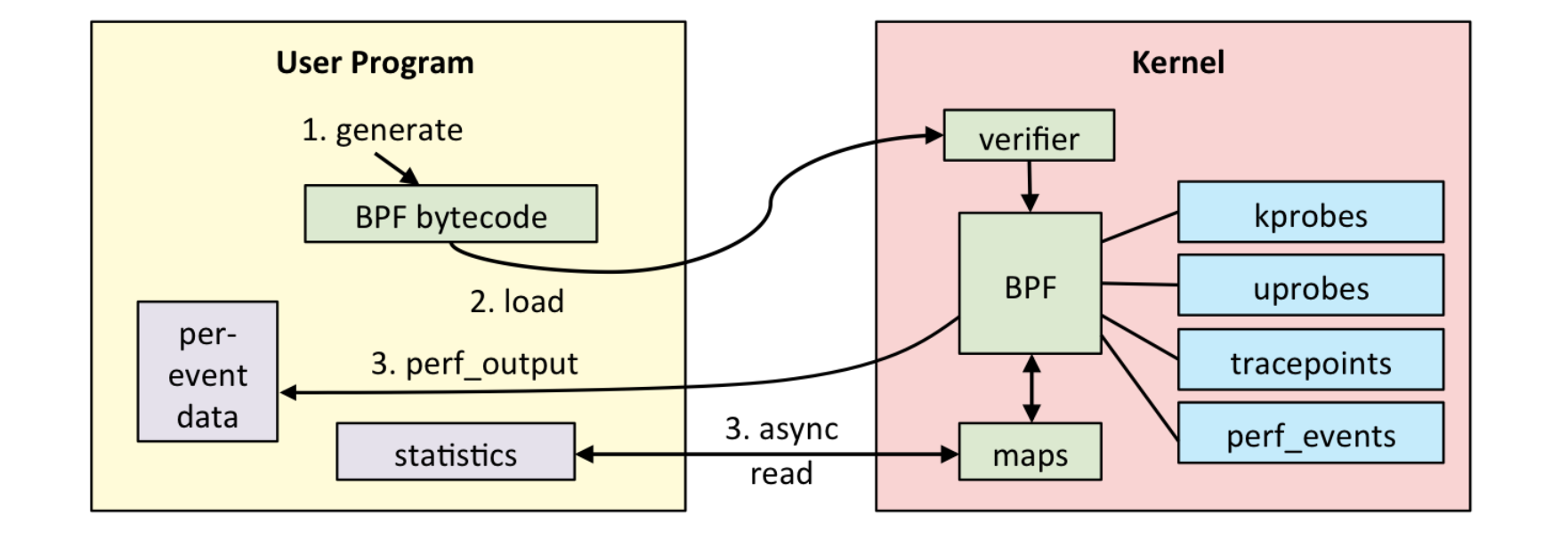
eBPF(Extended Berkeley Packet Filter,扩展的伯克利数据包过滤器)是Linux内核中的一种高效、灵活的程序执行框架。它允许在内核空间运行一些小型、受限制的程序,从而在不修改内核代码的情况下实现对内核行为的观察、修改和扩展。eBPF最初是为了实现高效的网络数据包过滤而设计的,后来扩展为一种通用的内核执行引擎,广泛应用于性能分析、安全监控、网络处理等领域。
eBPF可以认为是内核模块即LKM的替代,可以实现几乎全部的LKM模块的功能。eBPF有以下主要特性:
- 安全性:eBPF程序在加载到内核之前需要经过验证器(Verifier)的检查,确保程序状态的有限性,即没有不可控循环且不会访问非法的内存区域,所以eBPF在内核空间中执行时超级安全,永不崩溃
- 高性能:eBPF程序由一组简单的RISC指令组成,可以在内核中以JIT (即时编译) 的方式执行,接近于原生代码的性能,但因为多了更多边界检查与指令校验所以总体上要比LKM的性能差一些
- 可编程性:eBPF程序可以使用C语言编写,并通过LLVM编译器生成eBPF字节码,并且现在有了支持Go、Python等能用语言的框架
- 可扩展性:eBPF程序可以访问内核中的辅助函数 (helpers)来与内核交互,通过内存映射 (maps)可以实现应用层与内核层之间的通信交互和高效的数据共享
eBPF最大的好处就是安全性,即使出错也不会导致系统崩溃。另外,它解决了LKM多内核版本适配的问题,eBPF程序在BTF的加持下可以同一个二进制文件运行在多个内核之上。不过实际使用中,eBPF还是无法全量替代LKM,其限制相当多,主要是对内核版本的依赖,毕竟eBPF子系统还在开发中。eBPF框架主要有以下限制:
- 功能限制:为了确保内核的安全和稳定性,eBPF程序的状态必须是有限的,早期版本不支持循环,在编译时必须将循环做展开处理,而5.3之后才能支持Bounded loop,即常量次数的循环。eBPF程序不能直接访问内核内存或执行任意内核函数,只能调用eBPF的内核辅助函数(helpers),故其在功能上大大受限;另外为了安全考虑不能进行指针运算
- 指令限制:eBPF程序由一组限定的64位RISC指令组成,这些指令不支持浮点数、向量操作或高级控制结构 (如异常处理);eBPF指令是无架构的,故不能访问硬件寄存器或端口。从指令体系上来说其处理能力远不如x86或ARM等系统;5.2之前的内核所支持的最大指令数为4K,之后的内核最大支持1M指令数
- 内存限制:eBPF程序可以使用有限的堆栈空间和预分配的内存映射(maps),但不能使用其他内存资源 (如内核堆或全局变量); 函数堆栈只有512字节,函数调用层级亦不能多于9层,参数不能多于5个
- 系统限制:尽管eBPF框架在较新的Linux发行版中得到了支持,但在较旧的内核版本或特定的系统配置下依然无法使用或功能受限;其对内核版本依赖性较高,eBPF的功能及特性可能因Linux内核版本的不同而有较大的差异
- 性能开销:eBPF虽然是为高效场景服务场景设计的,但为了保证安全性引入了较多限制及检查,这些额外的动作均会引入性能开销,所以就性能指标而言比LKM要差
- eBPF程序必须遵循GPL协议
目前已有众多的安全安全产品及数据可视化平台正在使用eBPF框架以采集内核及网络事件,如Cilium、Sysdig、Tracee、KubuArmor等。
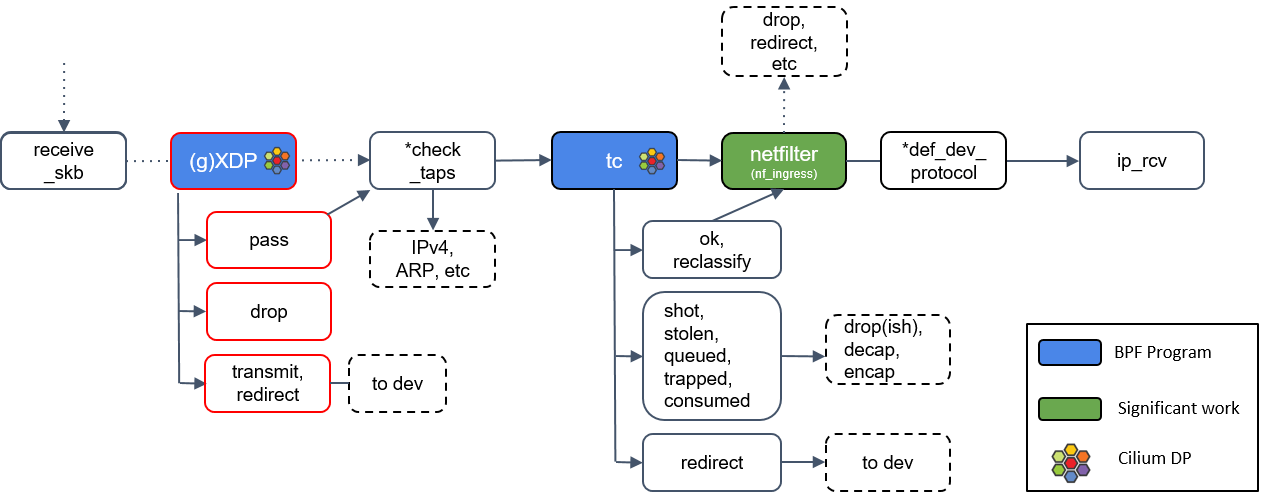
4.8 Netfilter & XDR
Netfilter框架自Linux 2.4.x时便并入了内核,是Linux网络功能及防火墙的实现基础,提供了网络数据包过滤的强大能力。应用层的交互由iptables或nftables完成。netfilter项目提供数据包过滤、网络地址(和端口)转换(NAT/NAPT)、数据包日志记录、用户空间数据包排队和其他数据包操作功能。

Netfilter实现了包过滤及防火墙功能,可通过iptables或nftables定义及下发规则。另外Netfilter允许内核模块在Linux网络堆栈的不同位置注册回调函数,当数据包到达Linux网络栈中预定位置时便会触发这些回调以通知内核模块进行下一步的处理。
XDP全称是eXpress Data Path (快速数据路径),基于eBPF指令的流程处理程序,其快速的原因在于能够在网络数据包到达网卡驱动时对其进行处理,具有传统框架所不具备的处理时机上的优势及更强的上下文识别能力,故最终可以达成较高的数据面处理性能。传统的Linux内核网络协议栈更强调和注重通用性,所以框架本身就固有性能瓶颈问题,特别随着如100G高速网络的出现,这种性能瓶颈就变得更加突出了,而基于eBPF的XDP程序则没有这些限制,所以XDP能够提高网络数据包的处理速度,同时减少内核协议栈的开销,并最终能够提升系统整体性能。
XDP 技术可以用于各种网络应用的实现,如入侵检测、流量监控、网络加速等各个方面。
5 安全领域实践 - Elkeid
5.1 Elkeid项目简介
Elkeid 是一款可以满足主机、容器与容器集群,Serverless 等多种工作负载安全需求的开源解决方案,源于字节跳动内部最佳实践。随着企业的业务发展,多云、云原生、多种工作负载共存的情况愈发凸显,故Elkeid项目就是我们推出的用以满足不同工作负载下安全需求的完整解决方案。
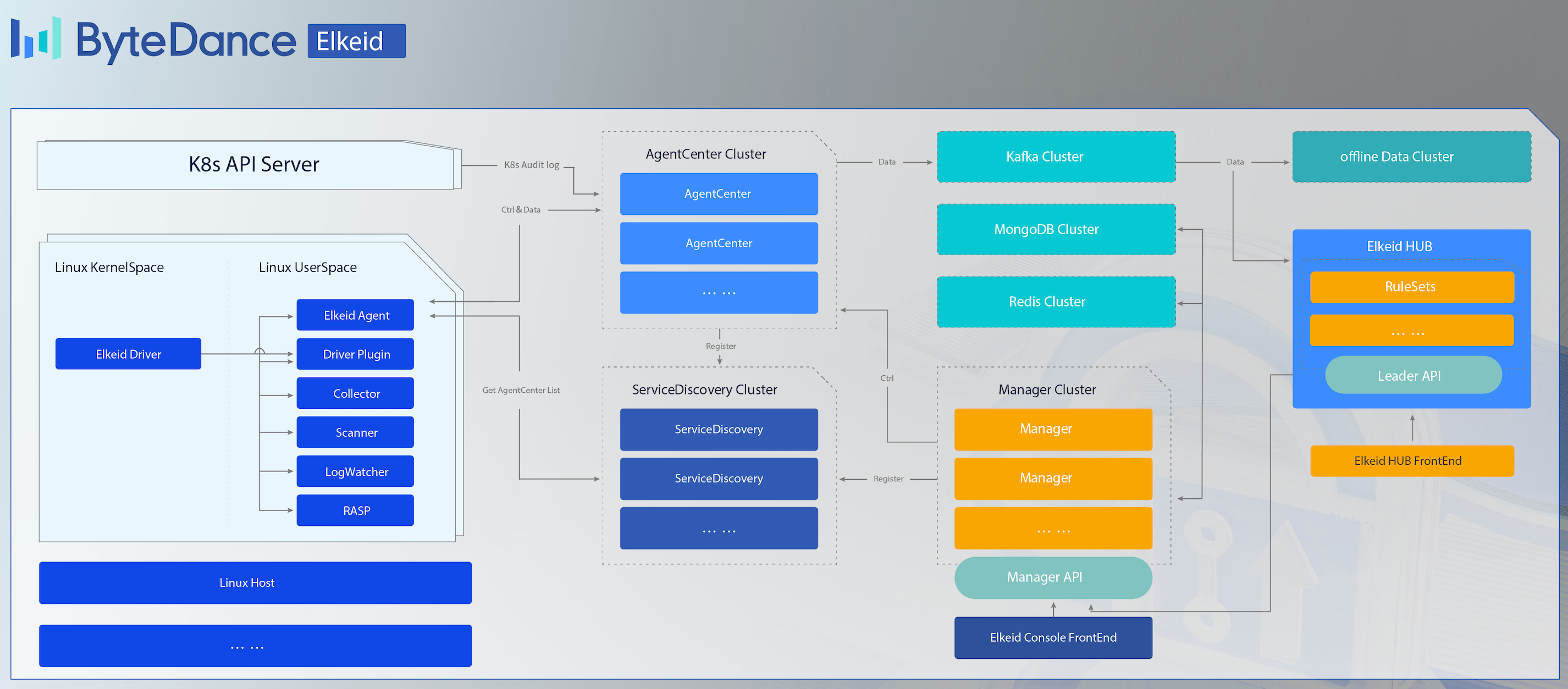
Elkeid 具备以下主要能力:
- Elkeid 不仅具备传统的 HIDS(Host Intrusion Detection System) 的对于主机层入侵检测和恶意文件识别的能力,且对容器内的恶意行为也可以很好的识别,部署在宿主机即可以满足宿主机与其上容器内的反入侵安全需求,并且 Elkeid 底层强大的内核态数据采集能力可以满足大部分安全运营人员对于主机层数据的渴望。
- 对于运行的业务 Elkeid 具备 RASP 能力可以注入到业务进程内进行反入侵保护,不仅运维人员不需要再安装一个 Agent,业务也无需重启。
- 对于 K8s 本身 Elkeid 支持接入K8s Audit Log 对 K8s 系统进行入侵检测和风险识别。
- Elkeid 的规则引擎 Elkeid HUB 也可以很好的和外部多系统进行联动对接。
Ekeid 将这些能力都很好的融合在一个平台内,满足不同工作负载的复杂安全需求的同时,还能实现多组件能力关联,更难得的是每个组件均经过字节跳动海量数据和多年的实战检验。本文里我们仅关注内部模块的实现,对Elkeid有兴趣的读者可访问Elkeid的网站或联系我们以便更详细地了解Elkeid项目。
5.2 监控点选择
Elkeid是主机安全产品线的监控能力,不需要阻断,即HIDS产品,非HIPS。目前Elkeid主要监控了33个高风险操作,其中18个默认开启,其它的只在沙箱模式下才会启用。监控点列表如下:
|
监控点或 |
编号 |
备注 |
启用 |
| 1 |
write |
1 |
|
|
| 2 |
open |
2 |
|
沙箱 |
| 3 |
mprotect |
10 |
only PROT_EXEC |
沙箱 |
| 4 |
nanosleep |
35 |
|
沙箱 |
| 5 |
connect |
42 |
|
开启 |
| 6 |
accept |
43 |
|
沙箱 |
| 7 |
bind |
49 |
|
开启 |
| 8 |
execve |
59 |
|
开启 |
| 9 |
process exit |
60 |
|
沙箱 |
| 10 |
kill |
62 |
|
沙箱 |
| 11 |
rename |
82 |
|
开启 |
| 12 |
link |
86 |
|
开启 |
| 13 |
chmod |
90 |
>= v1.8 |
开启 |
| 14 |
ptrace |
101 |
only PTRACE_POKETEXT or PTRACE_POKEDATA |
开启 |
| 15 |
setsid |
112 |
|
开启 |
| 16 |
prctl |
157 |
only PR_SET_NAME |
开启 |
| 17 |
mount |
165 |
|
开启 |
| 18 |
tkill |
200 |
|
沙箱 |
| 19 |
tgkill |
201 |
>= v1.8 |
沙箱 |
| 20 |
exit_group |
231 |
|
沙箱 |
| 21 |
memfd_create |
356 |
|
开启 |
| 22 |
dns query |
601 |
|
开启 |
| 23 |
create_file |
602 |
|
开启 |
| 24 |
load_module |
603 |
|
开启 |
| 25 |
update_cred |
604 |
only old uid ≠0 && new uid == 0 |
开启 |
| 26 |
unlink |
605 |
|
沙箱 |
| 27 |
rmdir |
606 |
|
沙箱 |
| 28 |
call_usermodehelper_exec |
607 |
|
开启 |
| 29 |
file_write |
608 |
|
沙箱 |
| 30 |
file_read |
609 |
|
沙箱 |
| 31 |
usb_device_event |
610 |
|
开启 |
| 32 |
privilege_escalation |
611 |
|
开启 |
| 33 |
port-scan detection |
612 |
tunable via module param: psad_switch |
沙箱 |
选择监控点的考量因素:
监控点并非越多越好,诚然数据种类越多越容易关联起来以提升发现攻击行为的检测水平,但同时也要考虑增加监控点的负担,综合起来的因素有以下3个:
- 高危操作:尽量覆盖,同时要避免相互间的重叠,即遵循MECE法则 (Mutually Exclusive, Collectively Exhaustive)
- 性能影响:不同的监控点及不同的回调处理对性能的影响均是不同的,需要实地测试评估
- 数据量:数据量的问题需要考虑部署规模,如果部署量为百万级,则每增加一个监控点最终所汇聚的数据可能将是巨量的,假设新增的一个监控1分钟产生一条1K的数据,则整个系统每分钟会增加1000000 * 1K = 1G的数据量,每天则会增加1.4T。
5.3 监控机制选择
在监控机制的选择上有两个核心考量维度:
-
通用性:跨度多个发行版(CentOS/RHEL/Debian/Ubuntu/SLES等)、多个内核版本(从2.6.32 - 6.4),多种CPU架构(AMD64、AArch64、RISC-V64)
- 性能因素:尽量降低对性能的影响,一般以5%为性能损失上限
从以上两点出发,同时又能保证监控点定制上的弹性,故做出以下选择:
主选:Tracepoints优先,并尽可能用 raw_tracepoint/sys_exit
- 可以处理64位系统下32位程序的syscall调用,通过检查TS_COMPAT标志判断
- 可以获取syscall及tracepoint调用点的所有信息,pt_regs或相应参数
- 尽量少的设置监控点,毕竟sys_enter或sys_exit均会接管所有的syscall,会有全局性的影响,在裸系统上设置sys_enter或sys_exit hook约带来3 - 5%的性能损失。ebpf的tracepint hook最终会向系统注册 perf_syscall_enter或perf_syscall_exit来接管所有的sys_enter及sys_exit事件,并在回调内部增加了分拣机制及相应的封装
备选:使用Kprobe或Ftrace,尽量避免Kretprobe
- kprobe的提供的API更友好;ftrace机制的普适性更好,但差别并不大,kprobe底层是优先选择ftrace来实现的
- kretprobe存在性能问题,高频或热点函数一定要避免kretprobe;较新内核kprobe机制已优化,但相比tracepoint还是较重
- 要注意的是kretprobe的ebpf回调中pt_regs全是乱值,与LKM的kretprobe的语义不一致,故kretprobe回调中如果想访问被hook函数的原始参数的话,只能通过kprobe先保存至map,然后kretprobe再从map中查询并获取相应的原始参数
最新的Elkeid的驱动模块及eBPF版本均以Tracepoints为首选监控机制,部分利用Tracepoints无法满足的监控点则使用了kprobe及kretprobe。
6 参考链接
6.1 Open Source & Linux
OS01 Rebel Code: Linux And The Open Source Revolution 2002, Glyn Moody
OS02 What Unix Gets Right
6.2 Linux Tracing
LT01: Linux Tracing Technologies, 6.5.0-rc2
LT02 Linux Tracing Concepts, 2021, Elena Zannoni
LT03 BPF, Tracing and more, 2017, Brendan Gregg
LT04 LWN: Unifying kernel tracing, 2019, Steven Rostedt
LT05 Linux Performance Analysis and Tools, 2013, Brendan Gregg
LT06 Linux Tracing Systems, 2017, Julia Evans
LT07 Choosing a Linux Tracer, 2015, Brendan Gregg
LT08 动态追踪技术漫谈,2016,章亦春
LT09 万字长文解读 Linux 内核追踪机制, 2023, 张帆
LT10 Linux Kernel Tracing, 2016, Viller Hsiao
6.3 Ftrace
FT01 Ftrace Kern elHooks: More than just tracing
FT02 Kernel Document: Function Tracer Design, 6.5.0-rc2
FT03 通过Ftrace实现高效、精确的内核调试与分析, 2023
6.4 Kprobes
KP01 Kernel Probes (Kprobes)
6.5 Linux Perf
LP01 Linux profiling with performance counters, 2023
LP02: perf Examples
LP03: Linux Perf Tools Tips, 2023, Oliver Yang
6.6 eBPF
eBPF @ Wikipedia
eBPF BPF Features by Linux Kernel Versions
LH01: LSM BPF Progams, 6.5.0-rc2
6.7 BCC
BC01: Systems Performance: Enterprise and the Cloud, 2e, Brendan Gregg
[BC02 BPF Performance Tools, 2019](https://www.brendangregg.com/bpf-performance-tools-book.html
BC03: eBPF Tracing Tools
6.8 bpftrace
BT01 A thorough introduction to bpftrace, 2019
BT02 bpftrace @ github
6.9 SystemTap
ST01 Getting started with SystemTap, 9.0
ST02: Using SystemTap for Dynamic Tracing and Performance Analysis, 2007, Mike Mason
ST03: SystemTap For Runtime Analysis of Kernel Modules such as AFS, 2015, IBM
6.10 LTTng
LT01 LTTng Project
LT02 LTTng Documents
LT03 How LTTng enables complex multicore system development, 2012, Manfred Kreutzer
6.11 DTrace for Linux
DT01 Orace DTrace
DT02 dtrace-linux@github
DT03 dtrace@fosdem
DT04 dtrace4linux@github: 由个人开发者PaulD.Fox维护的版本
6.12 Audit
AU01 Linux Audit Project, 2023
AU02 System Auditing, 6, RHEL
[AU03 Audit Your Linux Box, 2017](https://www.linux-magazine.com/Issues/2017/195/Core-Technologies
AU04 Syscall Auditing at Scale, 2017
AU05 go-audit @ github
AU06 What You Need to Know About Linux Auditing , 2022, Jakub Nyckowski
AU07 Linux audit详解, 2019
AU08 Syscall Auditing in Production with Go-Audit, 2018
6.13 uprobes
UP01 Uprobe-tracer: Uprobe-based Event Tracing, Srikar Dronamraju
UP02 Inode based uprobes, 2011, Srikar Dronamraju
UP03 Dynamic Instrumentation of User Applications with uprobes, 2019
6.14 Netfilter
NF01 netfilter.org project
NF02 In-depth understanding of netfilter and iptables, 2022
6.15 XDP
XD01 XDP @ github
XD02 Firewalling with BPF/XDP: Examples and Deep Dive, 2021
XD03 Get started with XDP, 2021
XD04 The BSD Packet Filter A New Architecture for User-level Packet Capture, 2017
XD05 L4Drop: XDP DDoS Mitigations
XD06 (译) 深入理解 Cilium 的 eBPF 收发包路径, 2019
6.16 Elkeid项目
BD01 Elkeid @ github


















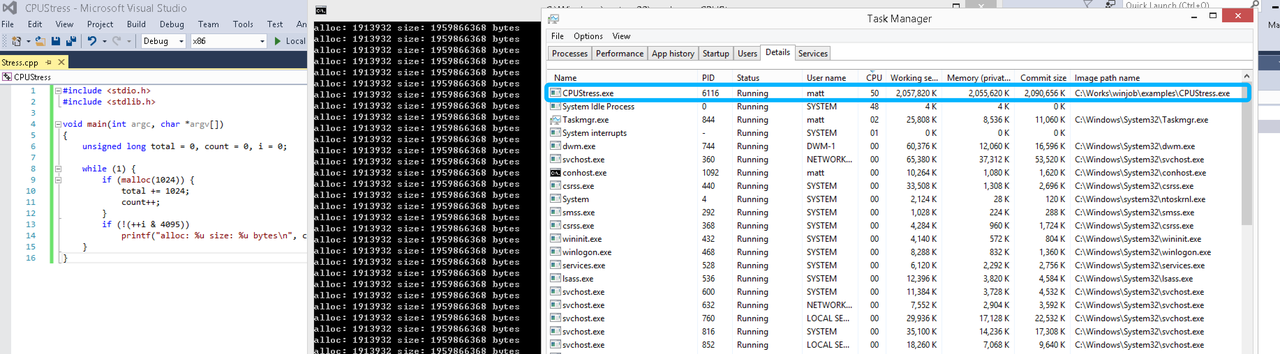
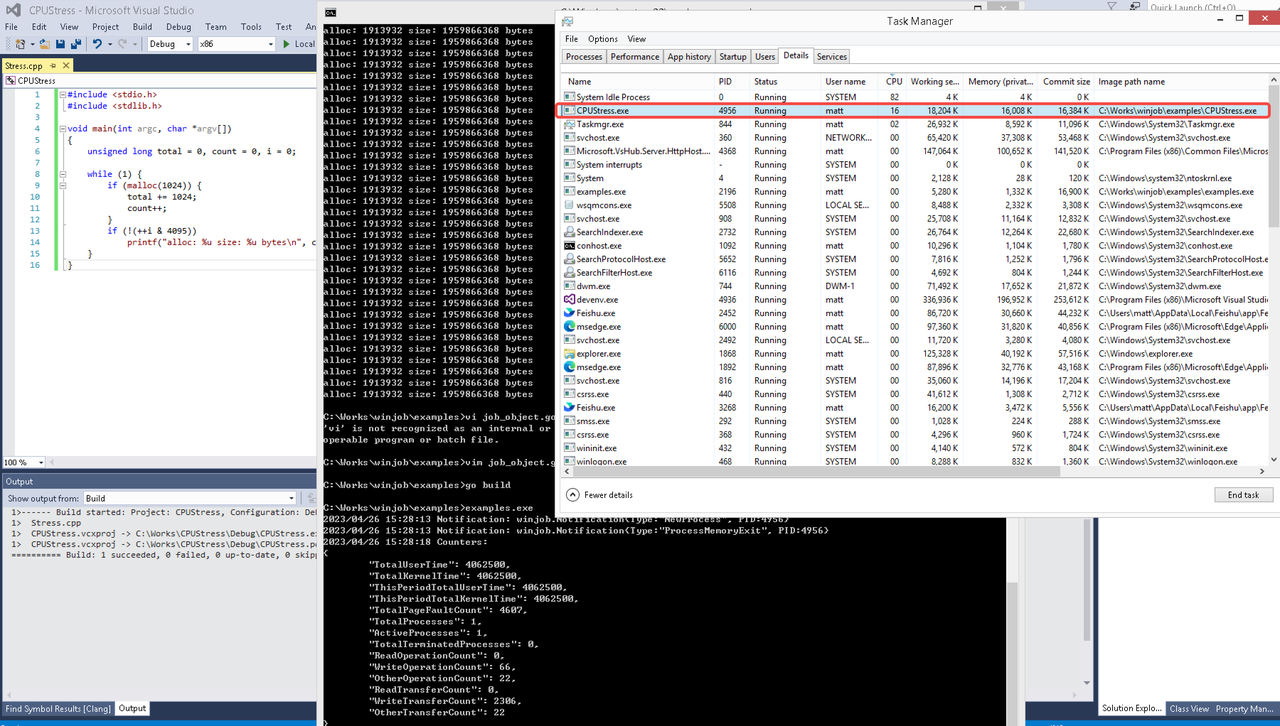 examples/job_object.go按如下修改:
examples/job_object.go按如下修改: